- bambano: Bambanő háza tája
- gban: Ingyen kellene, de tegnapra
- D1Rect: Nagy "hülyétkapokazapróktól" topik
- sziku69: Szólánc.
- Luck Dragon: Asszociációs játék. :)
- Geri Bátyó: B550 szűk keresztmetszet, de mi és miért?
- Szoszo94: Xiaomi Mi Router 3G - Padavanra fel!
- Chosen: Canon 5D II - portrézás 2025-ben
- Kempingezés és sátrazás
- sziku69: Fűzzük össze a szavakat :)
Új hozzászólás Aktív témák
-

#56474624
törölt tag
Átalakítod, hogy csak sin x, vagy csak cos x maradjon benne (ahol x természetesen lehet "2x" is, szóval egyetlen változó legyen, az a lényeg). Ehhez ismerni kell az összefüggéseket.
Pl. itt: ctg2x+tg2x=2
1/tg2x + tg2x = 2
1 + (tg2x)^2 = 2 tg2x
(tg2x - 1)^2 = 0
tg2x = 1
2x = pi/4 +k*pi (k € Z)
x= pi/8+k*pi/2 (k € Z)A másik még egyszerűbb, mert ott vagy sinx, vagy ctgx nulla, de sinx nem lehet az, mert akkor ctgx-nek nem lenne értelme (0-val osztás), ebből következően ctgx=0, azaz cosx=0, amiből x=pi/2+k*pi (k€Z).
Ezeknél természetesen van lényegesen nehezebb is. Amit tudni kell általában, az a sin(x+y) = sinx*cosy + siny*cosx, sin(x-y) = sinx*cosy - siny*cosx, cos(x+y) = cosx*cosy - sinx*siny, cos(x-y) = cosx*cosy + sinx*siny. Speciálisan sin(2x) = 2*sinx*cosx, cos(2x) = (cosx)^2 - (sinx)^2. Ezek ugye az előzőekből y=x behelyettesítéssel következnek. Általában igazából ezek fordulnak elő.
Ami még szokott lenni, az a sinx + siny, sinx - siny, cosx + cosy, cosx - cosy szorzatra való bontása, ezek igazából a fenti addíciós képletekből (így nevezzük őket) következnek, azokat most nem is írnám le. Ezutóbbit igazán integrálszámításnál lehet hasznosítani, összegre bontva a szorzatot, amit már könnyen tudunk integrálni.
-

wmati
addikt
Sziasztok
Trigonometrikus egyenleteknek megoldásának mi a menete ?
Pl: ctg2x+tg2x=2 vagy sinx*ctgx=0 -

HuMarc
veterán
válasz
 #56474624
#3197
üzenetére
#56474624
#3197
üzenetére
Igen, ezt a matektanár is mondta nekünk, hogy 1/3-mat ne váltsunk át 0,3 végtelen szakaszos tizedes törtre, hanem számoljunk törtekkel. (Mivel mind a négy alapművelet könnyebb törtekkel és végtelen szakaszos tizedes törtekkel amúgy sem lehet sem osztani, sem szorozni, sem leírni a pontos végeredményt.
Köszi a segítséget!

-

#56474624
törölt tag
No legalább elméletileg tudod a módszert.

Gyakorlatban viszont nagyon-nagyon könnyű mérési hibát véteni, az soha sem lesz pontos, ezért nem szabad így nekiállni. Amit még érdemes megjegyezni, hogy ha csinálsz egy számítást matek feladatban, törtekkel érdemes számolni, tehát 5/3-ot nem szabad 1.67-ként venni, majd azzal számolni. Csak a végén szabad kerekíteni, de igazából legjobb ott is a legegyszerűbb törtalak. Ezt csak azért mondom, mert jóval idősebbeknél is látom, hogy közben kerekítenek, nem törttel számolnak, aztán természetesen nem jön ki a végén a jó eredmény. -

#56474624
törölt tag
Azért nem értettem a 125-öt, mivel én úgy láttam, hogy MNPR egy négyzet és a 125 nem négyzetszám
Itt ehhez még, hogy a négyzetszámnak olyan szinten van köze a négyzethez, hogyha a négyzet oldalai egészek (az adott mértékegységben), akkor a területe négyzetszám (az adott mértékegység négyzetében). De egyébként ebben a feladatban szóval nem említették, hogy a négyzet oldalai egész egységnyi hosszúságúak.
A megméréshez pedig annyit, hogy egyrészt ezt soha nem fogják elfogadni egyetlen matematika feladatnál sem.
 Másrészt egész biztosan rossz következtetésre jutottál a mérésből. Azaz leméred vonalzóval, kapsz egy eredményt cm-ben/mm-ben. Csakhogy nem abban kérdezték, hanem az általuk megadott egység hosszúságban. Tehát le kellett volna mérned azt is, és azzal osztani a négyzet oldalának a cm-ben lemért hosszát, akkor kaptad volna meg az általuk megadott egységben.
Másrészt egész biztosan rossz következtetésre jutottál a mérésből. Azaz leméred vonalzóval, kapsz egy eredményt cm-ben/mm-ben. Csakhogy nem abban kérdezték, hanem az általuk megadott egység hosszúságban. Tehát le kellett volna mérned azt is, és azzal osztani a négyzet oldalának a cm-ben lemért hosszát, akkor kaptad volna meg az általuk megadott egységben. -

#56474624
törölt tag
c rész alapján MAR háromszög területe 5*10/2. Ebben semmi pith. nincs.
Aztán 4* terület(MAR háromszög) + 25. De ezt már leírták.
Amúgy nem semmi, hogy ugyanezt a felvételit iratják azokkal is, akik fazekas c osztályba (spec. matekra) mennek. Persze aztán szóbeli kiszűri, de jól emlékszem, hogy én is anno mennyire örültem, hogy nem kellett 8.-osként szóbeliznem, csak írásbeliznem. Írásban jobban tudtam érvényesülni. Így viszont ezt a lehetőséget elveszik. Nem tudom, kinek az ötlete volt ez a központosítás, sokkal izgalmasabb feladatok voltak régebben egy-egy ilyen felvételin, pláne a fazekasén.

-

HuMarc
veterán
-

Jester01
veterán
Tulajdonképpen te is elmondhatnád miért gondoltad, hogy 11.
Nézd valamelyik derékszögű háromszöget aminek a négyzet oldala az átfogója, például RDP.
RD=5 és DP=10 így Pitagorasz tétel alapján RP^2=RD^2+DP^2=125.MOD: Ha PItagoraszt még nem tanultad akkor add össze a háromszögek és a belső kis négyzet területét. 4*(5*10/2)+5*5=125
-

HuMarc
veterán
Akkor most a Pitagoraszból gyököt egy hatodikos szintjén is el tudnád mondani?
A többit sajnos értem

@Ba cy lus (#3190): Oké, ebből semmit nem értettem. A Pitagorasz-tételt ismerem (a^2+b^2=c^2) de én úgy tudtam, hogy csak nyolcadikos anyag.
Egyébként köszi a segítséget

-

HuMarc
veterán
Sziasztok!
 Pénteken felvételiztem, a megoldókulcs már kint van és egy pontot nem értek.
Pénteken felvételiztem, a megoldókulcs már kint van és egy pontot nem értek.Itt van maga a feladatlap. a 3. feladat d) pontjára én 121 területegységet írtam válaszként, mivel MNPR sokszög egy oldala 11 egység. 11×11=121.
De a megoldókulcsban a válasz 125 és azt írja, úgy kellett megoldani, hogy C×4+25. Az lenne a kérdésem, hogy miért.
Előre is köszönöm

-

axioma
Topikgazda
Nezd meg a szamokat, neki NEM az kell. Mert amiket sorolt mint megoldasok, azok mind az 1xn teglalap atloinak hosszai. Mondjuk nem artott volna az absztrakt problema helyett az eredetit vazolni, vagy ha feladatkent volt leirva, akkor a pontos szoveget megadni, mert igy ne csodalkozzon, hogy nem jo valaszt kap a nem jo kerdesre. Gyakorlatilag van az f(x)=gyok(x^2+1) fuggvenye, es kivancsi arra a g(y,z)-re, hogy g(f(x),z)=f(z). Mondjuk ez igy meg az altalam irtnal is rosszabb, mert ott f(x)-et es x-et is felhasznaltam, tehat vagy harom valtozossa tesszuk g-t, vagy ott a kozepen valahogy kiszedjuk... mindketto megoldhato persze, es ha ez nem szepsegdijas, hanem eredmenycentrikus excel, akkor lepesekben me'g konnyebb, az x explicit megadasa nelkul. Sajna ez se derult ki.
De persze mind1, latom meggyozni ugyse lehet, hogy leirt egy hamis egyenloseget, neki az tetszik, akkor ugy jo...energy4ever: Ja, ha excel, akkor ne negyzetosszegezzel, mert nagyon nem ide valo, hanem hatvany(1.41;2), azt erti mindenki. [Igen, ugyanazt az eredmenyt adja, mert egy mezore vegzed, de logikailag nem illik ide.]
-

Alg
veterán
válasz
 energy4ever
#3184
üzenetére
energy4ever
#3184
üzenetére
Leírtam lentebb:
Mit kell vele csinaljak, hogy 2 negyzetmeter atlojat(elvileg 2,23m) kapjam?
Megszorozni gyök2-velmit kell csinaljak 2 negyzetmeter atlojaval, hogy 3 negyzetmeter atlojat(elvileg 3,16) kapjam.
Elosztani gyök2-vel és megszorozni gyök3-alMit kell vele csinaljak, hogy X negyzetmeter atlojat kapjam?
1,41-et (ami egyébként gyök2 kerekítve) meg kell szorozni gyökX-el
-

energy4ever
addikt
Inkabb nekifutok a kerdesnek megint.
Adott egy negyzetmeter atloja(elvileg 1,41m). Mit kell vele csinaljak, hogy 2 negyzetmeter atlojat(elvileg 2,23m) kapjam? A megoldas legyen helyes arra is, hogy mit kell csinaljak 2 negyzetmeter atlojaval, hogy 3 negyzetmeter atlojat(elvileg 3,16) kapjam.Es en erre irtam ezt:
=gyok(negyzetosszeg(X)+1)
Tehat 2,23=gyok(negyzetosszeg(1,41)+1)Ha nem lenne egyertelmu, mivel excel-el van csinalva akkor megprobalom leforditani, vagyis:
Gyok((A)+1 negyzeten)
-

axioma
Topikgazda
válasz
 energy4ever
#3182
üzenetére
energy4ever
#3182
üzenetére
Negyzetosszege legfeljebb egy szamsorozatnak lehet.
De ugy nezem, igen, az lesz a jelentese nalad is, amit irtam az egymas melle tett negyzetekrol, az atlo gyok(negyzet(n)+1), ha igy jobban ismeros jelolesileg [bar a negyzetre emelest jobb lenne nem igy jelolni, ezt inkabb a geometriahoz kotjuk, mind1].
De hgoy a 3-bol 5-t az elozoben mit jelent es ez kell-e neked adott esetre, a pontosan megfogalmazott feladat nelkul nem tudom. Es azt se, hogy a kepletedbe belulre hogyan kerult bele az 1.41.
Esetleg!, ha mindig a kovetkezot vizsgalod, akkor nem egeszen jo, mert elobb kell az 1.41-bol a szelenek a hosszat megkapni, azaz negyzet(1.41)-1, majd ezt mint oldalt negyzetre emelni es az 1-et mint onmaga negyzetet hozzaadni, es az egeszbol gyokot vonni. Igy lehetne tehat esetedben:
2.23=gyok(negyzet(negyzet(negyzet(1.41)-1)+1)+1), ahol az elso +1 helyere ha +2, +3 stb. irsz, akkor a 2, 3 stb-vel tobb darabot megkapod. Vagyis pl. 4.16=gyok(negyzet(negyzet(negyzet(1.41)-1)+3)+1)Erre gondoltal?
-

Alg
veterán
válasz
 energy4ever
#3179
üzenetére
energy4ever
#3179
üzenetére
Azt átló a területtel gyökösen arányos, tehát ha a területet y-szorosára növeled, az átló gyök(y)-szorosára fog nőni.
1m oldalú négyzet átlója gyök2 hosszú. -

axioma
Topikgazda
válasz
 energy4ever
#3179
üzenetére
energy4ever
#3179
üzenetére
Hat ezt tenyleg nem sikerult, neki kene futni me'g egyszer.
Amire en ebbol asszocialtam: n darab negyzet egymas mellett hosszaban, es az igy kialakult teglalap atlojat keressuk, ami ugye gyok(1+n^2). Es az a kerdesed, hogy hogyan lehet kifejezni oket egymasbol, azaz a k.-bol a l.-et???
Az eredeti megfogalmazassal az a baj, hogy nincs olyan, hogy ket negyzetmeter atloja. Ezt legfeljebb ugy lehetne erteni, hogy a 2 nm teruletu negyzet atloja... mert ha 1x2-es teglalap, akkor mas az atlo, mintha gyok(2)xgyok(2) negyzet, a terulete meg ugyanaz. -

energy4ever
addikt
Sziasztok.
Akadt egy igen-igen bonyolult(legalabb is szamomra) kerdesem.
Adott egy negyzetmeter, melynek atloja X, mit kell csinaljak az X-el, hogy kijoljon 2 negyzetmeter atloja, de ugy, hogy az adott egyenlet igaz legyen pl 3-4 negyzetmeterre is.
Tehat egy olyan egyenlet kell amit elvegzek a 3 negyzetmeter atlojan, es kijon az 5 negyzetmeter atloja.
Sajnos nemtudtam helyesen megfogalmazni, de remelem valamelyik hozzaerto tud nekem segiteni.Koszonom elore is a segitseget.
-

axioma
Topikgazda
Sorry... neha kicsit tomenyen irok. A lenyeg, hogy a "hany variacio lehet az elso haton" szamolas kell ahhoz is, hogy a (7 alatt a 3) eseteket szetvalaszd az utolso szam alapjan - mert ugy ertettem, hogy ezt szeretned. Nincs olyan, hogy ebbol minden 4!-odik 2-es, vagy valami ilyesmit veltem kiolvasni a fejtegetesedbol.
-

axioma
Topikgazda
Ugy lehetne amit akarsz, hogy a 7!/(4!*3!) variaciokbol megnezed, hany esetben van 2-es es hany esetben 9-es a vegen, de lenyegeben azt fogod talalni, hogy a 6-os lehetseges tagok elofordulasatol fugg a ketto ara'nya amivel le kene osztanod (NEM 4:3, mert nem szimmetrikus!), vagyis nem uszod meg a 6-tal szamolast, akkor meg minek kavarni.
7! variacio ismetlesnel soha nem is volt, abbol nem lehet kiindulni, nem fuggetlen esemenyek szamjegyenkent. -

OgKush
senior tag
Áh köszönöm a válaszokat!
ÉS akkor gondolom ha 6 jegyű számot kell csinálni, akkor oda nem jó hogy 7!-6!, és az eredményt kivonom a 7!-ból.
Ez így nem jó mi? -

axioma
Topikgazda
-

Dave-11
tag
Tehát ugye van 7 darab számunk, és meg kell adni hogy ezekből hány darab 7 jegyű párost tudunk csinálni. Mi mindig felrajzolunk annyi vonalat, ahány számjegy van:
__ __ __ __ __ __ __ (pl. így)
Az utolsó helyre csak a kettes mehet, mivel ugye csak akkor lesz páros. Tehát a 7 rendelkezésre álló számból már csak 6 marad. Az első helyre tehát mehet 6 szám, a másodikra így már csak 5, mivel még egyet felhasználtunk, és így tovább. Tehát kijön hogy: 6*5*4*3*2*1*1 = 6! = 720 -

OgKush
senior tag
4db 2-esből és 3db 9-esből hány darab 7jegyű páros szám rakható ki?
Eljutottam odáig,, hogy ugye az utolsó szám az csak 2-es lehet, szóval hátul 4! állhat. Viszont innetől nem értem, hogy mit kell csinálni.
 valamiért nekem nem fekszik ez a kombinatorika
valamiért nekem nem fekszik ez a kombinatorika 
-

axioma
Topikgazda
válasz
 RoyalFlush
#3162
üzenetére
RoyalFlush
#3162
üzenetére
5. Akkor lesz bazis, ha nincsenek egy sikon. A sik az origo es a ket vektorvegpont altal meghatarozott sik, legegyszerubb talan felirni hogy ax+by+cz=d sikra mindharom illeszkedjen; mivel az origo kozte van, ezert d=0; a+b*2+c=0 es a*3+b*0+c*4=0, valamint az a-t valaszthatjuk 1-nek mivel az egyenletet konstanssal megszorozva is ugyanannak a siknak az egyenletet kapjuk (d=0 miatt), tehat legyen: 1+2b+c=0 es 3+4c=0. Na jo, jobb lenne a=4 valasztas.. szoval 4+2b+c=0 (nem kell megijedni, ilyenkor tok mas b,c jon ki, de ez nekunk mind1, ezek a 4-hez tartozoak lesznek, az elobbi egyenlettel lett volna az 1-hez tartozoak), es 12+4c=0. Vagyis b=-2 es c=-3, a sikunk egyenlete: 4x-2y-3z=0. Kerdes, hogy ezen mikor NINCS rajta a (0,3,M) pont (bocs, jelolesutkozes miatt atneveztem), 4*0-2*3-3*M<>0, M<>-2 barmelyik jo.
Azert a szamolasokat ellenorizd legy szives, mert ezt most csak igy gepen irogattam, az adatmasolasban es a fejbenszamolasban, atrendezesben is csinalhattam hibat. Ez mindegyik feladatra vonatkozik, nem csak erre! -

axioma
Topikgazda
4./c AC-re meroleges sik normalvektora az AC, azaz 1*x+0*y+(-1)*z=konstans, a D-n at kell mennie tehat D koordinatainak behelyettesitesevel a konstans -2, a keresett sik az x-z=-2 (vagy ha ugy jobban tetszik z=x+2).
Egyebkent ha az x,z koordinata-rendszerben abrazolod (y nelkul), akkor ez terlatasbol is jon. -

axioma
Topikgazda
válasz
 RoyalFlush
#3162
üzenetére
RoyalFlush
#3162
üzenetére
4.
BAD cosinusa: ki kell szamolni a hosszokat, es a cosinus-tetelt alkalmazni.
BA=gyok(3^2+1^2+2^2)=gyok(14) (a koordinatak kulonbsegebol jonnek a szamok)
AD=gyok(1^2+1^2+2^2)=gyok(6)
BD=gyok(4^2+0^2+3^2)=5 (az y=1 sikon pit. haromszog)
Most akkor c^2=a^2+b^2-2ab*cos(alfa), ahol cos(alfa)-t keressuk, c=BD
25=6+14-2*gyok(6*14)*cos(alfa)
-5/gyok(84)=cos(alfa), ez volt a kerdes (negativ, tehat tompasozgu, kis terlatassal talan latszik is, most nem rajzolgattam). Erdemes talan megjegyezni, ha ilyen a valasz, hogy ez lehetseges, mert -1 es +1 kozott van a cos(alfa) (nem hamis megoldast ad).ABC terulete: szemet kerdes, ujra kell kb. ugyanezt ABC-vel. Gyakorolj, csinald meg
 A cos(alfa) pedig azert jo nekunk, mert a szokasos sin2+cos2=1 valamint a haromszog szoge <180 feltetelbol megadhato a sin(alfa), az alfa szog melletti oldal hossza*sin(alfa) megadja, hogy mennyi az alfa masik szarahoz tartozo magassag (ha lerajzolod, sztem trivialisan latszik). A terulet tehat az alfa szog melletti ket oldalhossz szorzata szorozva sin(alfa)-val osztva ketto.
A cos(alfa) pedig azert jo nekunk, mert a szokasos sin2+cos2=1 valamint a haromszog szoge <180 feltetelbol megadhato a sin(alfa), az alfa szog melletti oldal hossza*sin(alfa) megadja, hogy mennyi az alfa masik szarahoz tartozo magassag (ha lerajzolod, sztem trivialisan latszik). A terulet tehat az alfa szog melletti ket oldalhossz szorzata szorozva sin(alfa)-val osztva ketto.
Egyebkent lehet a Heron-kepletet is hasznalni, amugy nagyjabol ennek segitsegevel jon le, kerdes hogy ebbe a feladatsorba illik-e mint megoldasmodszer. Az csak ennyi, az a,b,c oldalhosszokbol, es az s=(a+b+c)/2 felhasznalasaval: T=gyok(s*(s-a)*(s-b)*(s-c)). -

OgKush
senior tag
Sziasztok!
Van egy olyan feladatom, hogy (n+2)!/n! ezt hozzam egyszerübb alakra, itt gondolom nem lehet csak úgy felszorozni n!-al, nem?

-

axioma
Topikgazda
válasz
 RoyalFlush
#3162
üzenetére
RoyalFlush
#3162
üzenetére
1. x^4=16, x=2*(cos(90*k)+i*sin(90*k)), ahol k=0,1,2,3 (huuuuu, de regen volt!!!)
2. =(x^2+x+1)(x^2+x+1)^2012-1=(x^2+x)*(x^2+x+1)^2012+(x^2+x+1)-1, az elso tag elso tenyezoje oszthato (x-szerese), a masodik es a -1 osszeadasa soran ismet
3. Ha beszorzod az egeszet x^9-nel, akkor keressuk az eredmenyben az x^9 egyutthatojat. A kifejezes meg igy sozl: (2x^4+1)^9. Ebben nyilvan nem lesz x^9 egy darab sem. [Remelem ugyanazt ertem a feladat alatt, mint a felado tanar.]Folyt. kov., most mennem kell.
-

RoyalFlush
őstag
No, lenne néhány feladat, amiben szeretném egy gyakorlottabb segítségét kérni

1. Oldja meg trigonometrikus alakban az 2x^4-32=0 (X eleme C) egyenletet.
2. Igazolja, hogy x+1 osztja P(x)=(x^2+x+1)^2013-1 polinomot.
3. Adott E(x)=(2x^3+1/x)^9. Írja fel E(x) binomiális kifejezésének azt a tagját amelyik nem tartalmaz x-et.
4. Adott A(1,2,4) B(4,1,5) C(2,2,3) D(0,1,2) (pontok)
a) Számítsuk ki BAD által bezárt szög cosinusát.
b) ABC háromszög területét.
c) Írja fel AC egyenesre merőleges D ponton átmenő sík egyenletét.5. Írja fel x-et úgy, hogy a b c vektorok a térnek egy bázisát alkossák.
a(1,2,1) b(3,0,4) c(0,3,x) (vektorok)Köszönöm előre is!

-

Jester01
veterán
válasz
 concret_hp
#3160
üzenetére
concret_hp
#3160
üzenetére
A hiéna meg ugye haverokkal jön vissza és elkergeti az oroszlánt

-

Jester01
veterán
válasz
 FerNandor
#3155
üzenetére
FerNandor
#3155
üzenetére
Az oroszlán egy óra alatt 1 zebrát eszik meg, tehát x óra alatt x zebrát.
A gepárd 3 óra alatt 1 zebrát eszik meg, tehát x óra alatt x/3 zebrát.
A hiéna 6 óra alatt 1 zebrát eszik meg, tehát x óra alatt x/6 zebrát.Közösen tehát x óra alatt x + x/3 + x/6 zebrát esznek meg és 1 zebra van, tehát amit összesen megesznek az 1 zebra. Innen van az x + x/3 + x/6 = 1 ahonnan x = 2/3 óra = 40 perc. Ez idő alatt az oroszlán a zebra 2/3-át eszi meg (x), a gepárd a zebra 2/9-ét (x/3) a hiéna pedig a zebra 1/9-ét (x/6), így tehát összesen 2/3+2/9+1/9 ami valóban kiadja az egy szerencsétlen zebrát.
-

FerNandor
őstag
válasz
 FerNandor
#3153
üzenetére
FerNandor
#3153
üzenetére
amúgy nem pontosan értem. kicsit szájbarágosabben elmondhatnád, hogy mit mivel, hova helyettesítünk be.
szomorú, de ez a magyar felsöoktatás, ha olyat tanul az ember. nincs semmi matek. a legalapvetöbb dolgokat úgy elfelejtem, mint a huzat. pl múltkor hirtelen nem tudtam, hogy hogy szorzunk írásban.. nagyon durva.na látod..
 kifejtenéd akkor?
kifejtenéd akkor? -

Jester01
veterán
válasz
 FerNandor
#3151
üzenetére
FerNandor
#3151
üzenetére
Az oroszlán 1 zebra per óra sebességgel eszik, a gepárd 1/3 a hiéna pedig 1/6.
x óra alatt tehát összesen x + x/3 + x/6 zebrát esznek meg, és mivel 1 zebra van így innen x már adódik.Ha a rövidebb a hosszabb 2/3-a akkor a hosszabb a rövidebbnek 3/2-szerese (reciprok). A kettő összege pedig 90cm, tehát x + 3x/2 = 90.
-

FerNandor
őstag
hali,
segítség kéne, egy csomót felejtettem matekból.
milyen egyenletet kell felírni/hogy lehet megoldani a következö feladatokat?1. Egy oroszlán, egy gepárd és egy hiéna esznek egy zebrát. Az oroszlán 1 óra alatt enné meg egyedül, a gepárd 3 óra alatt, a hiéna 6. Ha együtt esznek, mennyi idö alatt eszik meg a zebrát.
2. ez a másik: van egy 90m-es csö. úgy kell felvágni, hogy az egyik a másiknak a 2/3-a legyen. Milyen hosszú a kisebb darab?
-

axioma
Topikgazda
Csak az evek kellenek oda-vissza? Mert akkor nem csinalom a nagy kereszttablazatot. Az akkor kene, ha kozben olyanokat is at akarnal forditani, mint hogy 2.5 ora.
Amugy nekem egybol a Sziriusz kapitany sorozat ugrott be, a holdon SOL xx - NOX xx szabvany idopontmegjeloles mellett me'g mindig emlegettek a "hetfon haromkor" alakot is - es erre nem igazan a regeny cselekmenye miatt volt szukseg, hanem mert az olvaso igy tudott idoben tajekozodni... -

fps8
senior tag
válasz
 PumpkinSeed
#3147
üzenetére
PumpkinSeed
#3147
üzenetére
 Ez kedves. Íme egy kis ízelítő.
Ez kedves. Íme egy kis ízelítő. -

fps8
senior tag
válasz
 concret_hp
#3145
üzenetére
concret_hp
#3145
üzenetére
Sosem használtam. Fenn van a gépen, de még azt sem tudom h mit hová kell beírni...
-

fps8
senior tag
Teljesen igazad van, az első probléma gépelési hiba. Most néztem a papíron nekem is 37 van.
Igen, az átváltásokra pedig egy olyan táblázatot kéne felállítani, amivel szükség esetén könnyen meg tudjam határozni egy egyén korát pl. mind két világ számításai szerint. Sajnos az excellhez meg nem értek
Elég az év és l. év szintjéig elmenni... nagyjából úgy, hogy mondjuk 10 l.év ~ = x év x hónap... -

axioma
Topikgazda
Egyreszt ellentmondasos ket sorod, vszinu 1 l. honap = 37 l.nap kene legyen a 36 helyett.
Masreszt most azt (olyanokat) kene irni, hogy 1 valos foldi ev az mennyi lenti ev tizedestorttel?En a helyedben felirnam egy excel tablaba ezeket az atvaltasokat, kifejeznek mindent 1 lenti napban (egy helyen megadod, a tobbit meg mar keplettel), majd csinalnek egy olyan ketdimenzios tablat, aminek mind a ket iranyban mind a ketfele naptarrendszer fel van irva es a keresztezo cellaban a fentibol listabol a napban kifejezett ertekeiket (megfelelo iranyban) osztanam. Ahol nagyon kicsi szam jott ki, azt ugyse fogod igy kifejezni egy regenyben; ha meg a tortresz is erdekes mert mondjuk 3.765 alak jon ki lenti napban valamire (exhas), meg mindig csak egy darab szorzas a 0.765-ra az alatta levo egyseg valtoszamaval - nagyobb pontossag ugyis megolne a regenyt...
Ha nem vilagos, szolj, legfeljebb szakitok kis idot megcsinalni, csak most nem erek ra ennyire.
-

fps8
senior tag
Pici változtatás az előző hsz-hez a pontosság kedvéért. Az arány amihez mérni kell:
10 lenti nap = 7,96 földi napnak felel meg. -

fps8
senior tag
Na, most már van valamim.
Ha: (l.- azt jelenti hogy lenti, tehát l.nap - lenti nap)
1 l.év = 740 l.nap
740 l.nap = 20 l.hónap
1 l.hónap = 36 l.nap
1 l.nap = 50 l.óra
1 l.óra = 100 l.perc
1 l.perc = 100 l.másodperc
és
1,25 l.nap = 1 nap
Akkor hogy váltom át a lenti időszámítást, földi időszámításra? Melyik esetnél mi a váltószám? -

fps8
senior tag
Azt hiszem el kell először teljesen vonatkoztatnom a földi időszámítástól, különben beleveszek... Kitalálom először hogy hogy legyen lenn, és aztán majd összevetve kitaláljuk együtt a 'váltókat'.

Ez tűnik a legegyszerűbbnek. -

fps8
senior tag
Nem. 74-hónapjuk van összesen, és 73 sötét. 1-hónap 10 napos, és 10 nap alatt 2-napot töltenek alvással.
Bár talán jobban szeretném azt, hogy ez a 10 napos ciklus 1 hétnek feleljen meg, és legyen még egy nagyobb intervallum is.
Azért kell hogy földi adatokkal is összeegyeztethető legyen, mert a regény a 2 faj találkozásáról, és azoknak következményeiről fog szólni. -

fps8
senior tag
Ugye a testüknek is szüksége van regenerálódásra, attól függetlenül hogy nincs éj/nappal váltakozás. Ezért vezettem be azt, hogy akkor egy egységnyi idő alatt (1/74) 10x alszanak... és átlagosan a 'napjuk' 20%-át alusszák át (ez lenne a 0.2, míg az embereke 0.25 tehát a 6-órával 25%-ot alszunk át de hosszab 1 napunk mint nekik). Na és innen hogyan tovább?
-

fps8
senior tag
Valami mégsem jó, mert 10-egységre akartam felosztani a 8-napnyi időt...
Az a baj hogy kicsit már keveredésben vagyok a fogalmakkal.
Mondom a tényeket. A vénusz 581-nap alatt éri el a 'világítós' időt, és az 8 napig tart. Tehát egy 589-napos periódus felel meg náluk 1-évnek. A világítós időszakot felosztottam 10-re úgy, hogy tekintve nekik 10*5 óra alvásra van szükségük ezen időszakban. Szóval a világítós idő 1/10-e felel meg 1 napnak.
Jól gondolom?
Ja és még plusz infó (a pontatlan adatok miatt) hogy a világos idő 1/74-e a teljes (589-napos) periódusnak. -

fps8
senior tag
Igen, csak annyi különbséggel hogy e lények esetében nincs nappal és éjszaka váltakozás, mert a föld alatt élnek és nem tudnak a felszínről. Ja és nem másik bolygón, hanem a földön, illetve a föld köpenyében.
A sztori szerint, a Vénusz amikor közel vana földhöz, hat egy erő a földre ami lenn (az ő világukban) egy kőzeten változást hoz létre. Gyakorlatilag világít. Ez a világítás ideje arányaiban, 74x fér bele a sötét állapot idejébe...Azt a rész amit kiemeltél, nagy valószínűséggel hibásan írtam le, de úgy számoltam ki hogy lenti időszámítás szerint 5x alszanak 5-földi órának megfelelő időt ~ 8-földi nap alatt, ami náluk 10 egységre van felosztva. Tehát a földön 8*6=48 órát alszanak 8nap alatt ami 8*24=192 tehát itt elosztottam a 48/192 (órát) és így jött ki 0,25.
-

Alg
veterán
Szia
Nem teljesen értem ezt az 1/1,2 meg 1/1,25-öt, de nem is érdekes...
Szerintem onnantól hogy meghatározod az adott bolygó tengely körüli forgásának idejét (1 nap*: éjszaka-nappal ciklusok) és keringési idejét (1 év*: évszak-ciklusok) a többi (hány óra* egy nap*, stb.) már csak technikai jellegű dolog, esetleg adott kultúrához lehet kötni valahogy... de matematikai szempontból tökmindegy.
*: természetesen nem földi, hanem ottani értelemben (pl. ha jól értem nálad egy év*=1,6 földi év)
-

fps8
senior tag
Sziasztok.
Írok egy regényt, és a regényben írt nép időszámításához kell egy kis számolási segítség.
Adott egy időperiódus jelzésére használt szakasz. Ez fel van osztva 74 egyenlő részre, ami hozzávetőlegesen 1.6 földi év hosszúságának felel meg. (ez a legnagyobb mértékegységem, nevezzük 'A'-nak)
A következő egység az A/74 - legyen 'B'.
Azt is kiszámoltam, hogy ezek a 'lények' 1B intervallum alatt 10x alszanak rendszeresen, és egy átlagos B szakasz 1/1,2-ét alusszák át 10 alkalomra bontva. Ez hozzávetőlegesen 8-nap a földön, és mi földiek ennyi idő alatt alszunk átlagosan 8*6 azaz 48 órát ami a szakasz 1/1,25-e. Tehát ebből következik hogy ők rövidebb időt alszanak ~ 5 órát de többször, ergo 8-földi nap alatt 10x.
Most itt tartok, és lövésem sincs hogyan oszthatnám tovább.
El szeretnék menni a másodperc nagyságrendjéig az időmérésben...
Javaslatokat várok. Nem baj ha légből kapott, csak csatlakozzon valahogy a rendszerhez és abból már tudok alkotni valamit.
Szerk: ja és ha persze valahol tévedek akkor elnézést
 Kicsit már bele vagyok zavarodva a témába...
Kicsit már bele vagyok zavarodva a témába... 
-

Dave-11
tag
Ha van egy szamsorozat, amelynek minden tagja 1, akkor annak az also es felso korlatja is 1, es akkor mondhatjuk ra hogy korlatos?
-

Phvhun
őstag
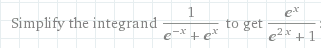
Hogy lett az 1.ből a 2.?
-

#56474624
törölt tag
Álljunk meg, az ugyanannyi nem volt benne az eredeti szövegben, az volt benne, hogy mindegyikének annyit ad, mint ami, ez pedig nem sugall az égvilágon semmit ugyanannyiról. Mennyit ad? Annyit, mint ami a nála lévő pénz negyede. Akkor lenne egyértelmű, ha azt mondanák, hogy az épp nála lévő pénz felét adja oda a másik kettőnek egyenlően elosztva, abban az esetben nem lehetne belekötni. Így igen, mert a pénzadásnak lehet egy sorrendje a valóságban (ha már felhoztad, hogy a nem egész tallér nem túl reális), nem feltétlen egy időben zajlik.
-

axioma
Topikgazda
válasz
 #56474624
#3123
üzenetére
#56474624
#3123
üzenetére
Azert normalis ember az ugyanannyit - hacsak nem eleve ma'r ara'nyokban beszelunk - alapbol a valos mennyisegre erti. [A lanyom magyar felveteli feladatsort oldott meg gyakorlasbol, szovegertes, oda van irva szovegbe hogy csak akkor indulnak kirandulni ha van 35 jelentkezo; alul kerdes hogy lehetnek-e 33-an? Mire beirja, hogy igen, mert 33-an lehetnek azt lehet ugy is erteni, ahogy a honapos(*) feladvanyt... szerintem nem ertekeltek volna, ha valos helyzetben beir egy ilyet.]
(*) Az evben 4 honap 30 napos, 7 honap 31 napos. Hany honapban van 28 nap? -

axioma
Topikgazda
válasz
 #56474624
#3121
üzenetére
#56474624
#3121
üzenetére
Nem tartom valoszinunek, az hogy "a masik ketto mindegyikenek" annyit ad, nekem sugallja eleve, hogy mindketten egyformat kapnak. [Azon el nem hanyagolhato aprosagon felul, hogy igy az adott eszkoztarral megoldhato a feladat, elagazasok nelkul, mert a tiednel az se lenne mindeyg, melyiknek ad elobb.]
Nos, ha visszafele kezded el nezni, akkor egybol az jonne, hogy a 16 az 3/4-e annak, mint ami az utolso kulon atadas elott volt, es 1/3 penzt elegge mesebeli penzrendszerekben ismernek csak
-

#56474624
törölt tag
válasz
 ngabor2
#3115
üzenetére
ngabor2
#3115
üzenetére
A feladat szövege félreérthető számomra, ugyanis ad a másik kettő minegyikének negyedannyi pénzt, mint ami épp nála van.
Tehát az is egy eshetőség, hogy először odaadja az egyiknek a negyedannyit, majd a másiknak a maradékból negyedannyit. Kezdetben tehát ha volt neki A, egyiknek 0.25A-t, másiknak 0.25*0.75A-t ad. Na igen, csak hogy ekkor amikor kapják a pénzt, az nem teljesen egyértelmű, hogyan.

-

axioma
Topikgazda
válasz
 ngabor2
#3115
üzenetére
ngabor2
#3115
üzenetére
En ezt visszafele csinalnam.
1. A harmadik lepes utan 16-16-16 akkor amelyik eppen osztott, annal 32 volt (fele maradt), 8-8-at adott, tehat a harmadik osztozkodas elott 8-8-32 volt.
2. A masodik lepes (biztos nem a 32-es, o a harmadik oszto lesz) utan az osztozkodonak 8 maradt, akkor 16 volt, 4-4-et adott. Vagyis ezen osztozkodas elott 4-16-28 kellett legyen.
3. Az elso lepest az tette, akinek utana 4 maradt, tehat 8 volt, 2-2-t adott, vagyis a kiindulas 8-14-26.Az ugyan nyilvanvalo, hogy csak ebben a sorrendben osztozkodva jon ki belole a 16-16-16, de ezt nem is kerte a feladat, hogy barhogy keverhessek egymast.
-

ngabor2
nagyúr
mert feladat

az első kettőből kijött egy oldal levezetés után, hogy B=2,5A, C=48-2,5A, de itt véget is érnek a (majdnem) egész számok. valahol valamit elrontottam...
ha a 3. hosszú egyenletet is megoldom, akkor se jön ki szebb.
37A + 20B + 16C = 1024
13A + 36B + 16C = 1024
5A + 4B + 16C = 512 -

ngabor2
nagyúr
ismét egy általános iskolás versenyfeladat, de sikerült levezetésben alaposan elbonyolítanom...
3 vándor találkozik, mindegyiküknél van valamennyi pénz. Az egyik ad a másik kettő minegyikének negyedannyi pénzt, mint ami épp nála van. Ezután a másik 2 vándor is ugyan ezt teszi. Végül mindhárom vándornál 16-16 tallér lesz. Hány tallér volt a leggazdagabb vándornál találkozásukkor?
úgy kezdtem, hogy van a 3 vándor (A, B, C). A+B+C=48
az első adakozás után:
1: 0,5A
2: 0,25A + B
3: 0,25A + C2. kör:
1: 0,5A + 0,25(0,25A + B)
2: 0,5(0,25A +B)
3: 0,25A + C + 0,25(0,25A + B)3. kör:
1: 0,5A + 0,25(0,25A + B) + 0,25(0,25A + C + 0,25(0,25A + B))=16
2: 0,5(0,25A +B) + 0,25(0,25A + C + 0,25(0,25A + B))=16
3: 0,5(0,25A + C + 0,25(0,25A + B))=16tehát van 4 egyenlet és 3 ismeretlen, elvileg megoldható lenne. csak mire mindezekből kifejezem valamelyiket, megőszülök.
persze lehetne kezdeni azzal, hogy mindent végigszorzok 32-vel, és akkor nincs tört. de valahogy úgy sejtem, hogy van egyszerűbb út is.
-

AND1
őstag
Sziasztok,
szükségem lenne egy jó matekosra.
Szűrő: akinek nem gond a fősulis matek 1-2, az írjon privit.
(természetesen honorárium fejébe)köszi!
-

axioma
Topikgazda
Akkor egy egydimenzios fuggveny is jo neked, a 2D-bol az jott le, hogy a keresett gorbe a koordinata-rendszerben nem feltetlen fuggveny. (Vagyis nalad az x koordinatai a pontoknak feltetlen kulonboznek, ez feltetel lesz.) Valamint az se volt vilagos, hogy neked polinom kell (ill. jo), akkor pedig 3 pontra egy (max.) masodfoku illesztheto, vagy vegtelen sok magasabb foku.
Itthagytam, mire megvacsoraztunk, a megoldasi modszer az elozo hsz-ban...
-

axioma
Topikgazda
-
-
Sziasztok!
Wolframalpha-ban nincs valamilyen levezetési mód, hogy lássam hogyan lehet eljutni a végeredményig?
-

PumpkinSeed
addikt
Áh értem, bár itt nekem inkább az angollal volt baj.

Új hozzászólás Aktív témák
Hirdetés
- Nyaralás topik
- Macska topik
- bambano: Bambanő háza tája
- Macron betiltatná az EU-ban a közösségi médiát a 15 év alattiaknak
- Nem várt platformon a OnePlus Nord 5
- Telekom otthoni szolgáltatások (TV, internet, telefon)
- Folyószámla, bankszámla, bankváltás, külföldi kártyahasználat
- gban: Ingyen kellene, de tegnapra
- Tőzsde és gazdaság
- D1Rect: Nagy "hülyétkapokazapróktól" topik
- További aktív témák...
- Honor Pad X8 64GB, Wi-Fi, 1 Év Garanciával
- 10% -tól elvihető. Országosan a legjobb BANKMENTES részletfizetés! Lenovo Legion Pro 7
- AKCIÓ! AMD Ryzen 7 3800X 8mag 16szál processzor garanciával hibátlan működéssel
- LG UltraGear Gaming Monitorok: FRISS SZÁLLÍTMÁNY -30%
- Beszámítás! Apple Watch SE 2024 44mm Cellular okosóra garanciával hibátlan működéssel
Állásajánlatok
Cég: CAMERA-PRO Hungary Kft
Város: Budapest
Cég: PC Trade Systems Kft.
Város: Szeged







 Másrészt egész biztosan rossz következtetésre jutottál a mérésből. Azaz leméred vonalzóval, kapsz egy eredményt cm-ben/mm-ben. Csakhogy nem abban kérdezték, hanem az általuk megadott egység hosszúságban. Tehát le kellett volna mérned azt is, és azzal osztani a négyzet oldalának a cm-ben lemért hosszát, akkor kaptad volna meg az általuk megadott egységben.
Másrészt egész biztosan rossz következtetésre jutottál a mérésből. Azaz leméred vonalzóval, kapsz egy eredményt cm-ben/mm-ben. Csakhogy nem abban kérdezték, hanem az általuk megadott egység hosszúságban. Tehát le kellett volna mérned azt is, és azzal osztani a négyzet oldalának a cm-ben lemért hosszát, akkor kaptad volna meg az általuk megadott egységben.














 valamiért nekem nem fekszik ez a kombinatorika
valamiért nekem nem fekszik ez a kombinatorika 
 A cos(alfa) pedig azert jo nekunk, mert a szokasos sin2+cos2=1 valamint a haromszog szoge <180 feltetelbol megadhato a sin(alfa), az alfa szog melletti oldal hossza*sin(alfa) megadja, hogy mennyi az alfa masik szarahoz tartozo magassag (ha lerajzolod, sztem trivialisan latszik). A terulet tehat az alfa szog melletti ket oldalhossz szorzata szorozva sin(alfa)-val osztva ketto.
A cos(alfa) pedig azert jo nekunk, mert a szokasos sin2+cos2=1 valamint a haromszog szoge <180 feltetelbol megadhato a sin(alfa), az alfa szog melletti oldal hossza*sin(alfa) megadja, hogy mennyi az alfa masik szarahoz tartozo magassag (ha lerajzolod, sztem trivialisan latszik). A terulet tehat az alfa szog melletti ket oldalhossz szorzata szorozva sin(alfa)-val osztva ketto.




![;]](http://cdn.rios.hu/dl/s/v1.gif) )
)







 Kicsit már bele vagyok zavarodva a témába...
Kicsit már bele vagyok zavarodva a témába... 


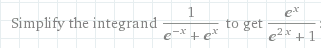
 Hidd el, hogy félreérthető. Az ember csak onnét gondolhatja, hogy nem erre gondoltak, hogy nem tudja megoldani.
Hidd el, hogy félreérthető. Az ember csak onnét gondolhatja, hogy nem erre gondoltak, hogy nem tudja megoldani. 








