- sziku69: Fűzzük össze a szavakat :)
- iPhone témaösszefoglaló
- Luck Dragon: Asszociációs játék. :)
- hcl: Kelj fel komám, ne aludjál
- sziku69: Szólánc.
- LordAthis: Ismét egy "Idióta" A.I. Projekt, hogy meglovagolja az aktuális trendeket...
- Geri Bátyó: Agglegénykonyha 1 – rizseshús másképp
- bambano: Bambanő háza tája
- Kalacskepu: Elrontott Radeon X1950 Pro megjavítása
- GoodSpeed: Bye PET Palack, hello SodaStream
Új hozzászólás Aktív témák
-

kispx
addikt
válasz
 PumpkinSeed
#5199
üzenetére
PumpkinSeed
#5199
üzenetére
Bolyai-sorozat.
-

PumpkinSeed
addikt
Utoljara az egyetemen fogolalkoztam matematikaval (Kalkulus, Diszkret matek, stb.), viszont mostanra annyira kiurult a matektudasom, hogy szinte semmi, van valami konyv ami szepen visszaraz az "alapoktol"? A vegcel kikepezni magam, hogy machine learning rendszerekkel tudjak foglalkozni, de nem csak ilyen TensorFlow-val hanem en magam is ertsem.
Szoval tulajdonkeppen egy vagy tobb konyvre lenne szuksegem.

-

lajafix
addikt
válasz
 bandi0000
#5186
üzenetére
bandi0000
#5186
üzenetére
Bolyai könyvek, Solt György: Valszám az ajánlott darab. Az elmúlt 10 évben beírtam soxor, feladat kinyomozni hogy milyen eloszlás szerint.
 . Ennél több nem kell, de tényleg rá kell szánni sok időt.
. Ennél több nem kell, de tényleg rá kell szánni sok időt.ne add fel a valszámot, 20 éves tapasztalatom, hogy a high end matek legjobban használható része a gyakorlatban.
-

axioma
Topikgazda
válasz
 Ghoosty
#5193
üzenetére
Ghoosty
#5193
üzenetére
Gyakorlatilag van olyan a kommutativ, egysegelemes gyurukben (egesz szamok, valos szamok, modulo maradekosztalyok stb.), hogy -1*-1=1.
Eloszor lassuk be, hogy a 0 mint additiv egysegelem a szorzasra zeruselem.
0+0=0 (mivel egysegelem, 0+x=x igaz barmely x-re, tehat x=0-ra is).
A disztributivitas miatt 0*x=(0+0)*x=0*x+0*x, hozzaadva a -(0*x) tagot (a 0*x additiv inverzet), 0=0*x.
Tehat ha a 0 szorzasra zeruselem, felhasznalva hogy a -1 (a multiplikativ egysegelem additiv inverze) hogyan van definialva: 0=0*x=(1+-1)*x=1*x+-1*x=x+-1*x. Ezzel bebizonyitottuk, hogy minden szam additiv inverze (mivel az egyertelmu, ez is kivarazsolhato) megegyezik a -1-szeresevel. Ebbol persze kovetkezik, hogy -1*-1=-(-1)=1 (behelyettesitve x=-1 -et).
Tehat ha a,b pozitiv szamok, akkor ellentetjuk (additiv inverzuk) a -a es -b mint negativ szamok szorzata igy nez ki: -a*-b=-1*a*-1*b=-1*-1*a*b=(-1*-1)*a*b=1*a*b=a*b. Jo, ehhez tudni kell, hogy a pozitiv szamok halmazabol nem vezet ki a szorzas... vagyis a*b pozitiv. De hat minden attol fugg, hogy hogyan vezeted be a "negativ szam" fogalmat... -

Ghoosty
őstag
Olvastam egy blogban tudománykommunikációval kapcsolatban egy hozzászólást, ami elgondolkodtatott.(A kiemelés a lényeg.)
"pl a DNS-re ami a hétköznapi életben csak nagyon áttételesen bizonyítható, miközben tízből kilenc ember azt sem tudja levezetni, hogy két negatív szám szorzata miért lesz pozitív."
Világ életemben jó voltam matekból, így teljesen magától értetődő volt ez, de mikor le akartam vezetni, hogy hogyan lesz két negatív szám szorzata pozitív, nem sikerült. Egyáltalán le lehet vezetni, vagy van ilyen axióma/axiómaszerűség, hogy -1*-1=1.
Ha ez létezik, akkor a szorzás asszociativitásából le tudom vezetni, bármilyen számra, de nem tudom, hogy ez az alap létezik-e.Keresve végül ilyen furcsa levezetést összehoztam:
-1x0=0
-1x(5-5)=0
-1x(5+(-5))=0
(-1x5)+(-1x-5)=0
-5+(-1x-5)=0
hogy megmaradjon az egyenlőség, akkor a (-1x-5)-nek 5-nek kell, hogy legyen. Eljátszhatjuk, hogy 5 helyett n van, de ez így nekem nem tetszik. -

#36268800
törölt tag
A Budapesti Corvinus Egyetemen mennyire durva a matek általánosságban pl. egy BME mérnökinfo-hoz képest, és mondjuk kifejezetten egy közgazdasági szakon?
-

bandi0000
nagyúr
köszönöm még1-szer , nekem sem a kedvenceim közé tartoznak ezek, vagyis a tanárom mondta jól, hogy ha ezzel foglalkoznánk, sok feladatot oldanánk meg, akkor leesne egyből hogy mit mivel hogyan, de így érintőlegesen nem a legjobb ezt tanulni
ha már ennyire szereted... hátha esetleg erre van ötleted még utoljára
 Holnap már ZH utána már engem sem fog érdekelni
Holnap már ZH utána már engem sem fog érdekelni 
diszkrét eloszlásoknál van a binomiális,geometriai, hipergeometriai ,és a bernoulli eloszlás, ezekre nem tudsz véletlen valamit, ami egyértelműen megkülönbözteti ezeket? nézegetem a feladatokat valamikor épp leesik hogy mivel kéne számolni, de valamikor csak akkor ha megnézem a megoldást
-

axioma
Topikgazda
válasz
 bandi0000
#5184
üzenetére
bandi0000
#5184
üzenetére
Jaj, a valszam amint nem kombinatorika vagy ilyen abrazolas, az ami a masodik legjobban ki tud kergetni a vilagbol matekon belul (diff.egyenletek utan). Az eloszlasfuggvennyel csak nagyon kezdo szinten vagyok tisztaban, arrol inkabb nem mernek tanacsadas formajaban nyilatkozni, plane altalanossagban.
De az atfogos szerintem: egy.szaru derekszogu gyok2-vel az az 1,1 szaru, az atfogobol nezve gyok2/2 magassagu haromszog, gyakorlatilag egyik oldala az f(x)=x integralja (x^2/2), a masik meg ugyanaz me'g eccer, felesleges felirni foleg a nem nullatol es nem a legegyszerubb alaku a fuggveny, inkabb duplazni kell mondvan ugyanaz tukrozve. Ja az integral azert, mert minden ponthoz "ossze kell adni" a tavolsagat az atfogohoz, olyan mint a szumma 1-tol n-ig, ennek folytonos altalanositasa az integral. Jobban nem tudom megmondani, hogy miert, ez ilyen "valoszinuleg ez kell legyen" nalam. Es a vegen osztani is kell az atlagos tavolsaghoz a gyok2 hosszal amin vegzed (vagy nem duplazol es a gyok2/2-vel, mind1). -

bandi0000
nagyúr
köszönöm, közben rá jöttem én is, de legalább kaptam egy kis megerősítést

viszont ha már itt..., akkor, valami tipp/trükk a folytonos véletlen változóhoz? értem hogy mit kell csinálni, csak az nem jön össze, hogy az alap eloszlás fügvényt nem nagyon tudom felírni, bár itt valszeg az a baj, hogy a legtöbb esetben geometrián alapul, pl volt egy olyan hogy, egyenlő szárú derékszögű háromszög átfogója √2 nagyságú talán, és a háromszögön belül véletlenszerűen kiválasztunk egy pontot, és az milyen messze van az átfogótol
-

axioma
Topikgazda
válasz
 bandi0000
#5182
üzenetére
bandi0000
#5182
üzenetére
Grafikon: x tengely ido (ertelemszeruen 18:00-18:30 kozott erdekes), y tengely "megtortenes valoszinusege", ide fogod mind a kettot abrazolni, skala 0 es 1 kozott.
Fogsz egy egyenest 1800 es 1830 kozott 0-rol 1-re novekvoen, meg egy masikat, 1820-1830 kozott 1-rol 0-ra csokkenoen (azt abrazolod, hogy a kutya meg nincs kiengedve) . A teljes valoszinuseg az elso alatti terulet, a "rossz" pedig ami ebbol mar a masodik fole eso darab, vagyis a kedvezo a ket vonal mindegyike alatti. Most nem szamolnam ki, de ezt a ket teruletet kell osztani egymassal (persze forditott sorrendben).
Ja remelem ertheto is, hogy melyik mit reprezental, ha nem akkor kerdezz vissza. -

bandi0000
nagyúr
sziasztok
tudna valaki segíteni geometriai valószínűségben?
nem túl bonyolult feladatok, de egyáltalán nem látom át a számunkra kedvező eseteket, pl apa hazaér véletlenszerűen 18:00 és 18:30 kor, a szomszéd kutyája 18:20 és 18:30 kor szabadul el véletlenszerűen, azt kell megmondani, hogy apa hamarabb érkezik mint a harapós kutya -

Jester01
veterán
válasz
 DeathBat666
#5180
üzenetére
DeathBat666
#5180
üzenetére
Ez sem tűnik bonyolultabbnak csak tudni kellene a jelölések mit takarnak.
-

ricinus13
senior tag
Sziasztok!
Ha van egy függvényem aminek a meredekségét lineáris regresszióval kell meghatároznom, és az x=0 értékhez is rendel valamilyen y értéket, akkor ugye az x(átlag)-ba a 0-t is bele kell vennem?
-

Jester01
veterán
válasz
 DeathBat666
#5175
üzenetére
DeathBat666
#5175
üzenetére
Ha novemberre 10%-al nőtt ami 14M Ft, akkor máris tudjuk, hogy júliusban 140M Ft volt és novemberben 154M Ft. Augusztus simán adódik 1,15*július miatt és december pedig egyenlő augusztussal. Szeptember az augusztus + 5MFt, október pedig november / 1,11. Ezzel az első oszlop kész, a többi számolható.
-

DeathBat666
aktív tag
Sziasztok, jövőhéten írok egy zh-t Statisztika 1-ből és nem értem ezt a táblázatos feladatot:
http://www.kepfeltoltes.eu/view.php?filename=582stat.jpg
nekem úgy tűnik, mintha túl kevés adat lenne hozzá, egyszerűen nem tudok rájönni, hogyan kéne megoldani.
előre is köszönöm a válaszokat!
-

axioma
Topikgazda
válasz
 Apollo17hu
#5172
üzenetére
Apollo17hu
#5172
üzenetére
Ez is jo, de szorgalmi feladatkent szerintem erre a "trukkos" megoldasra gondolhattak: ha a szam helyett a szam+1-et nezed, akkor az oszthato 5-tel, 7-tel es 9-cel. Az elso ilyen szam ezek legkisebb kozos tobbszorose, ami jelenleg - mivel relativ primek - a szorzatuk, 315. A keresett szam tehat csak a 314 lehet.
-

looser
addikt
válasz
 Apollo17hu
#5172
üzenetére
Apollo17hu
#5172
üzenetére
Köszönöm szépen, így érthető! Közben elküldtem egy ismerősömnek, aki szintén válaszolt, közzéteszem:
Első poén:
5 el osztva 4, 7-el osztva 6, 9-el osztva 8 -> ez máshogy fogalmazva: 5-el, 7-el és 9-el osztva is -1 a maradékAzután meg kell találni a legkisebb közös többszöröst:
5,7,9 relatív prímek: nincs - nél nagyobb közös osztójuk, ezért a legkisebb közös töbszörösük 5*7*9 =315
315-nek mindhárom az osztója ebből le kell vonni 1-et -> 314 a megoldás314 /5 = 62*5 + 4
314/7 = 44*7 + 6
314/9 = 34*9 +8Köszönöm újfent mindenkinek!
Üdv
-

Apollo17hu
őstag
Végül, hogy sikerült megértenem a feladatot, szerintem így lehetne megoldani:
- ha 5-tel osztva 4 a maradék, akkor a szám 4-re vagy 9-re végződik,
- ha 9-cel osztva 8 a maradék, akkor a számjegyek összege 9-cel osztva is 8 maradékot ad,
- 7-re vonatkozóan nincs oszthatósági szabály.Az első két feltétel alapján a pozitív egészek növekvő sorrendben:
44, 89, 134, 179, 224, ... 45*p - 1
...vagyis keressük azt a "45*p -1" alakban felírható legkisebb pozitív egész számot, ami 7-tel osztva 6 maradékot ad.
Egyenletben felírva, rendezve és prímtényezőkre bontva:
5*3^2*p = 7*q
Innen pedig következik hogy p-nek oszthatónak kell lenni 7-tel, tehát:
5*3^2*7 = 45*7 = 315 --> A keresett szám a 314.
szerk.: A 45*p - 1 alakra egyszerűbben rá lehet jönni az 5-ös és 9-es osztás feltételére felírt prímtényezős szorzatból, és nem kell a mire végződiket, meg a számjegyek összegét nézegetni.
-

skoda12
aktív tag
válasz
 Apollo17hu
#5169
üzenetére
Apollo17hu
#5169
üzenetére
Azért nem ennyire egyszerű, mert a 4-re így csak az első feltétel teljesül, a másik kettő már nem.
-

skoda12
aktív tag
Neked egy lineáris kongruenciarendszert kell felírnod és megoldani, majd a megoldáshalmazból a legkisebb pozitív számot kiválasztani. Kínai maradéktételre keress rá.
Egyébként ez a feladattípus azért jó, mert ZH-ban pont ugyanúgy lehet megoldani, amilyen módszerrel vizsgán a kínai maradéktételt bizonyítani lehet. -

looser
addikt
válasz
 Apollo17hu
#5165
üzenetére
Apollo17hu
#5165
üzenetére
Így szól pontosan a példa:
Határozd meg azt a legkisebb olyan pozitív egész számot, amely öttel osztva négy, héttel osztva hat, kilenccel osztva pedig nyolc maradékot ad.
-

looser
addikt
Sziasztok!
Hogyan kell megoldani a következő példát?
Melyik az a legkisebb pozitív szám (X), amelyet elosztva 5-tel, a kapott számon felül 4 lesz a maradék.
Ugyanez az X 7-tel elosztva 6 maradékot, 9-cel elosztva 8 maradékot kapunk.Üdv

-
Axioma szebben fogalmazott

-

axioma
Topikgazda
válasz
 #74220800
#5159
üzenetére
#74220800
#5159
üzenetére
Tisztazzuk: halmaz, vagy multihalmaz?
Halmaznal nincs olyan, hogy "ket darab ... van benne". A halmaz attol halmaz (es nem csak sokasag), hogy barmirol el tudjuk donteni, hogy benne van vagy nincs.
A halmazba bele tudsz ketszer rakni egy elemet, ha igy nezed (informatikai szemmel), vagy lehet "a listaban szereplo szamok halmaza" ahol a listaban ketszer szerepel, de a halmaz vagy tartalmazza, vagy nem.
Tehat ha halmaz, akkor a ket halmaz egyenlo, es benne egyetlen elem van: az 1-es.
Ha multihalmaz lenne, nehol van ilyen, akkor mindket operandus multihalmaz, es az eredmeny is az. Az eredmenyhalmaz ebben az esetben az 1-est 1x tartalmazo multihalmaz. -

#74220800
törölt tag
Ez eleg amatör kerdes lesz, de szeretnem tisztazni.
Van ket halmazom. Az egyikben ket darab 1es van a masikban egy.
A metszetben ekkor mi lesz? Egy vagy ket darab 1es?köszi,
-

Jester01
veterán
válasz
 BTminishop
#5157
üzenetére
BTminishop
#5157
üzenetére
Mi nem világos? A szinusz az 2 pi periódusú, tehát az n/2*pi az 4 féle értéket vehet fel, de abból most véletlenül kettő az nulla tehát ezért lesz 3 részsorozat.
-

BTminishop
aktív tag
sziasztok,
5.feladat itt a sinus mi alapján veszi fel az értékeket? nagyjából értem de jó lenne ha valaki kiegészítené.

-

BTminishop
aktív tag
válasz
 Orionhilles
#5155
üzenetére
Orionhilles
#5155
üzenetére
-
Sziasztok!
Matek fakt, trigonometria: 3sin(2x) + 2cos(2x) = 2
3sin(2x) + 2cos(2x) = 2 //0-ra redukálom, vagyis -2
3sin(2x) + 2cos(2x) -2 = 0 //cos(2x) = cos^2x-sin^2x
3sin(2x) + 2(cos^2x-sin^2x) -2 = 0 //cos^2x = 1-sin^2x
3sin(2x) + 2((1-sin^2x)-sin^2x) -2 = 0
3sin(2x) + 2(1-2sin^2x) -2 = 0
3sin(2x) + 2-4sin^2x -2 = 0
3sin(2x) -4sin^2x = 0 //sin2x = 2*sinx*cosx
6sinx*cosx-4sin^2x = 0
6sinx*cosx = 4sin^2x // kiemelem a 2sinx-etMindegy, már rájöttem, hol akadtam meg, a kiemelés résznél.

Kérdésem: Milyen tankönyvet/könyvet/feladatgyűjteményt/online valamit tudnátok ajánlani trigonometriában, amiben a megoldások részletezve vannak?
Egyelőre elég gyérül megy, leginkább az a gondom, hogy lassú vagyok, beletelik egy kis időbe amíg az azonosságokat felfedezem.
Válaszokat előre is köszi!

-

Dr. Mózes
aktív tag
Sziasztok! Az alábbi képletnek miért végtelen a határértéke? Ha a 2 a 3n-edikenből 8 n-ediket csinálok, és azzal végigosztok, akkor 0 lesz. Vagy ezt így nem szabad?
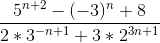
-

Rapido251
csendes tag
Nagyon szépen köszönöm a segítségeket! Nagyon jól jöttek, hálás vagyok értük!

-

Dinter
addikt
válasz
 BTminishop
#5149
üzenetére
BTminishop
#5149
üzenetére
A monotonitásnál még nincs is baj, de a korlátosságnál beragada 6-os mellé.
-

Dinter
addikt
Adott ez a rekurzív sorozat (zárójelben az index). A feladat bizonyítani, hogy konvergens. Ilyenkor csinálhatom azt, hogy veszek egy másik sorozatot, amiben elhagyom a mínuszos tagot, mivel 0-hoz konvergál, így lényegileg nem számít?
-

BTminishop
aktív tag
válasz
 BTminishop
#5146
üzenetére
BTminishop
#5146
üzenetére
Csak, hogy valami meg is maradjon benned leírom miről is van itt szó.
Rekurzív sorozatokról van szó, tehát az a sorozat n+1 edik elemét az a sorozat n-edik elemével állítjuk elő, ezért is rekurzív a neve. Az ilyen fajta feladatoknál azzal kell kezdeni, amit a papíron is írtam és ilyenkor megjelennek a lehetséges határértékek. Mivel a konvergencia feltétele, a monotonitás és a korlátosság ezért meg kell nézni, hogy a sorozat monoton nő vagy csökken és ezt bizonyítani teljes indukcióval.segédanyag 17.oldaltól
-

axioma
Topikgazda
válasz
 Rapido251
#5143
üzenetére
Rapido251
#5143
üzenetére
Kezdjuk ott, hogy a feladat nyilvan az, hogy a sorozat konvergal-e es ha igen, mi a hatarerteke...
Az "eddig jutottam"-ot nem ertem.
Az latszik, hogy a gyok c az fixpont (ha lehetne az a_i gyok c maga, akkor az a_i+1 is gyok c-re jon ki), de neked a konvergenciat kell belatni. Ehhez en a gyokc-hez kepest irnam fel az a_i-ket, es a kulonbseg minden hatar ala csokkenteset probalnam bizonyitani (pl. exhas hogy az elozo 3/4-enel nem lehet tobb).
De most sajna nincs idom vegigcsinalni. -

axioma
Topikgazda
OK, csak azt az elso vagy-ot is &-nek irtad, ezert nem volt egyertelmu.
DeMorgan-okkal:
A+(~A&B)=A+(~(A+~B))=~(~A&(A+~B))=~(~A&A+~A&~B)=~(~A&~B)=A+B
Lehet, hogy nem ez a legrovidebb, most csak irtam egy probalkozast.
Figyelem, a negalas vegig erosebb precedencianak van feltetelezve, mint az & es +!
Annyit hasznal fel, hogy ~(x&y)=~x+~y, ~(x+y)=~x&~y, ~(~x))=x, x+~x=0, 0+x=x. Ja es hogy x&(y+z)=x&y+x&z. Lehet, hogy ez vegulis a teljes paletta
-

axioma
Topikgazda
Nem ismerem ezt a jelolesrendszert... egyaltalan, halmazelmelet vagy mat.logika?
De szerintem elirtad, az azonossag amire asszocialtam: A unio (A komplementere metszet B) egyenlo A unio B, mat.logikaban A vagy (nem A es B) egyenlo A vagy B. De nalad az & kicsit megszaladt a bal oldalon (es a zarojel ha ugy lenne, asszociativitas miatt felesleges is lenne). -

Dinter
addikt
Az A&(~A&B) kifejezést hogy tudom algebrai átalakításokkal A+B alakra hozni? Nem tudok rájönni és egyszerűen nem hagy nyugodni.
-

Dr. Mózes
aktív tag
Sziasztok!
A BGE-n levelezőn elkezdtem tanulni az analízist, de teljesen el vagyok veszve. Pár hónapja elkezdtem a Khan Academy segítségével felfrissíteni a matekomat, mert kb. négy éve volt utoljára matek órám, de most úgy érzem, hogy semmit sem ért, amit ott átvettem.
Tudnátok ajánlani valamilyen oldalt/könyvet/bármit, hogy ne vágódjak el az első vizsgámon?
A Csernyák László féle Analízis tankönyvet ajánlotta a tanárunk, de teljesen kínai nekem, nem elég szájbarágós. -

axioma
Topikgazda
válasz
 K1nG HuNp
#5134
üzenetére
K1nG HuNp
#5134
üzenetére
Hat kicsit nemszivesen mondom ra, hogy igen. Mert a gyokvonas valojaban nem igazan muvelet a komplex szamokon (az i - nekem mar csak i marad - es a -i is negyzetgyoke a -1-nek), ebbol a szempontbol en is pongyola voltam. Csak hat ez a szokasos "segito" magyarazat.
A harmadik hatvany persze hogy az. Azzal mar forditva nincs gond: az i kobe a -i. Azert van benne 3. hatvany, mert a z-t mint osszeget kobre emelte (az (a-b)^3=a^3-3*a^2*b+3*a*b^2+b^3 azonossaggal), ezt kerte a feladat.
Egy picit nezz utana a komplex szamoknak, ha egyelore a polarkoordinatas nem is kell (bar abbol gyonyoruen latszik az i^3=-i), de a ketdimenzios ertelmezest mindenkepp. Szerintem wiki is eleg lehet bar most nem neztem ra, de jo lenne ha nem csak az adott feladatot tudnad megoldani, hanem ertened hogy mibol jon ez, miert igy kell ill. forditva, miert lehet igy szamolni ezekkel.Szerk.
Opsz, most latom, nem te voltal a kerdezo. De ha mar kerdes szintjeig erdekel, erdemes ranezni, nem egy hsz-ba belefero tema. -

scofield657
csendes tag
köszönöm
-

Jester01
veterán
válasz
 scofield657
#5129
üzenetére
scofield657
#5129
üzenetére
Hát ez triviális, csak be kell helyettesíteni aztán 0 lesz (vagy nem).
z^3=j^3-3j^2+3j-1=-j+3+3j-1=2j+2
z^2=j^2-2j+1=-1-2j+1=-2jz^3+4z^2+6z+4=(2j+2)+4(-2j)+(6j-6)+4=2j+2-8j+6j-6+4=0
Nyilván tudni kell hozzá a binomiális együtthatókat (vagy kézzel ki kell szorozni) meg persze azt, hogy j^2=-1
-

axioma
Topikgazda
Olyan ertelemben nem szabad egyszerusiteni sem, hogy a ket kifejezes mint lekepezes kulonbozo lesz, hiszen kulonbozo lesz az ertelmezesi tartomanya. Tehat az egyszerusitett melle bizony oda kell (illik) irni, hogy y!=2. Mas kerdes, hogy az adott feleletvalasztos tesztnel erre nemigen volt lehetoseg... azaz latszolag igeny se. Ma meg mar alt.suliban is tesztverseny van, mert azt egyszerubb javitani

-

lev258
veterán
válasz
 zsolti1debre
#5126
üzenetére
zsolti1debre
#5126
üzenetére
Egyszerűsíteni mindig lehet, osztani már csak feltételek mellett. A kikötés (vagy kikötések) csak a nevezőre vonatkoznak, viszont az egyszerűsítés által kicsit lazul (két kikötés helyett csak egy lesz).
-

csiben1
tag
Sziasztok!
Matematikából szeretnék újra érettségizni és ehhez keresek egy felkészítőkönyvet amivel lehetőleg egymagam el tudnék kezdeni felkészülni. Később természetesen mennék tanárhoz. Tudtok ajánlani olyan könyvet vagy könyveket ami nem csak feladatokat/megoldókulcsokat tartalmaz, de el is magyarázza az elméletet? -

Cucuska2
addikt
válasz
 overclockerr
#5115
üzenetére
overclockerr
#5115
üzenetére
Szia!
Nekem ez vált be nagyon.
-

overclockerr
tag
Sziasztok!
Szimplex módszerre keresnék egy normális leírást. Sajnos az előadóm nagyon siet, hadar, követhetetlen az egész. Félig már rájöttem, de kellene azért egy iromány hozzá.
Előre is köszönöm a segítséget!
-

axioma
Topikgazda
válasz
 zsolti1debre
#5112
üzenetére
zsolti1debre
#5112
üzenetére
Eloszor ki kell szamolni a kozepso resz burkologorbejet, aztan lehet a fuggvenyt (a ket kuppal egyutt) szepen integralod (Pi*int(f^2))
-

Cucuska2
addikt
válasz
 zsolti1debre
#5112
üzenetére
zsolti1debre
#5112
üzenetére
És mi a szögre vonatkozó paramétered?
-

zsolti1debre
tag
válasz
 Apollo17hu
#5104
üzenetére
Apollo17hu
#5104
üzenetére
Ha a kocka ele a,akkor a kapott forgastestnek,ami az animacion lathato vajon mennyi lehet a terfogata?
-

Doky586
félisten
válasz
 zsolti1debre
#5098
üzenetére
zsolti1debre
#5098
üzenetére
"egy tokeletes kocka alaku dobokockat megporgetunk"
Talán egy kicsit beugratós a kérdés.
Gondolom földi körülményekről van szó hogy egy asztallapon pörgetsz meg egy dobókockát, ezen esetben kizárólag akkor stabil a pörgés ha lapjával van az asztalon ---> így az eredmény egy henger.
De ha gravitációmentes helyen végzed a kísérletet (sör és pálinkamentes környezetben) akkor rengeteg más eredmény is elképzelhető, attól függően hogy a tengely hol 'szúrja át' a kockát.. és a tengely stabil-e vagy folyamatosan változik-e, mert ezen esetben akár gömb is lehet az eredmény.
-

Apollo17hu
őstag
válasz
 zsolti1debre
#5109
üzenetére
zsolti1debre
#5109
üzenetére
nehogy félreértsétek, nem én csináltam, csak gugliztam
mindenesetre érdekes feladvány -

zsolti1debre
tag
válasz
 Apollo17hu
#5104
üzenetére
Apollo17hu
#5104
üzenetére
Koszonom mindenkinek a megoldasokat!Azt sajnos elfelejtettem irni,h a kocka a csucsan porog.Mentsegemre szolgaljon,h egy kocsmabol irtam.Az animacion levo "megoldas" nagyon tetszik,szep munka!Mutattam a kerdesfelrakonak,azt mondta,h ez a helyes megoldas!

-

axioma
Topikgazda
Marpedig valamiert csak az van, hogy a tavoli vitorlasnak eloszor csak a tetejet latod, es ugy latsz belole egyre tobbet, ahogy kozeledik... Keresztben a Balaton mondjuk 10 km alatt van (atuszasi tav 5.2km), es ugye a szemlelo kb. 1.5m-en levo nezopontjat is bele kene szamolni, kerdes hogy a tulparti kikoto hajoibol mit lat. Mert hogy a tulpart hegyeit latja, az semmi, mert nem tudja hogy az amit o a vizszinten levonek "lat", a tulparton mennyivel van a vizszint felett. De egyebkent szkeptikusunk fogjon egy ismerost, menjen at a ket partra es reflektorozzanak egymasnak, mikor latjak mikor nem.
-

Kloden
senior tag
Sziasztok, ezzel a lapos föld elmélettel kapcsolatban mondta az egyik hívő, hogy a Balaton 70km-én a Föld görbülése egyik végétől a másikig 400m lenne ha gömb alakja lenne a Földnek. Ezt valaki meg tudná erősíteni? Mert én kiszámoltam derékszögekkel, és nekem is 400m jött ki, ami elég durva, mert látszani meg nem ez látszik.
Valaki ki tudná számolni ezt körívvel is? Én ahhoz nem értek Föld sugár 6300km, Balaton hossz 70km legyen.
Föld sugár 6300km, Balaton hossz 70km legyen. -

axioma
Topikgazda
válasz
 Apollo17hu
#5104
üzenetére
Apollo17hu
#5104
üzenetére
Szep!
-

axioma
Topikgazda
válasz
 Apollo17hu
#5101
üzenetére
Apollo17hu
#5101
üzenetére
Szerintem a ket kup kozott nem lesz az henger, inkabb valami hiperbolikus felulet. Mert ha a tengellyel parhuzamos lenne a szakasz akkor persze igaz lenne, de ez keresztben megy, es a tengelytol valo tavolsaga nem marad vegig egyforma (ki lehet szamolni a csucsoknak es ezen koztes elek kozepenek a testatlotol valo tavolsagat).
-

Apollo17hu
őstag
válasz
 zsolti1debre
#5098
üzenetére
zsolti1debre
#5098
üzenetére
Ha lapján forog, akkor henger, ha élén, akkor két összeillesztett csonkakúp, ha pedig "szabályosan" a sarkán, akkor szerintem két olyan kúp, ami hengerrel kapcsolódik egymáshoz. Azért jön létre a henger, mert az a két csúcs, ami a forgástengelyt határozza meg, 3-3 másik csúccsal van összeköttetésben, ezek viszont 1-1 külön síkot határoznak meg (ezek a síkok a henger alapjai).
Ez talán segít kicsit a gondolkodásban.
Új hozzászólás Aktív témák
- Gamer egerek és billentyűzetek kitűnő árakon! Most extra 10% kedvezmény!
- 0% THM 6 havi részlet, beszámítás! Gamer PC, notebook, konzol, Apple termék, hardver KAMATMENTESEN!
- BESZÁMÍTÁS! MSI B450M R5 4500 16GB DDR4 512GB SSD RTX 1660Ti 6GB ZALMAN S3 FSP 500W
- Gamer PC-Számítógép! Csere-Beszámítás! R7 2700 / RX 5500XT 8GB / 16GB DDR4 / 256SSD + 1TB HDD
- Samsung Galaxy S23 Plus / 8/512GB / Kártyafüggetlen / 12 Hó Garancia
Állásajánlatok
Cég: FOTC
Város: Budapest





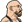
































![;]](http://cdn.rios.hu/dl/s/v1.gif)

 Megpróbálom azt, amit mondtál.
Megpróbálom azt, amit mondtál.