- gban: Ingyen kellene, de tegnapra
- sziku69: Szólánc.
- sziku69: Fűzzük össze a szavakat :)
- Luck Dragon: Asszociációs játék. :)
- Meggyi001: Nyilvános wc-k.....még mindig hiánypótló...
- Meggyi001: Anya, tudsz segíteni a matekban?....Nem érek rá kisfiam, majd segít a ChatGPT...
- bitpork: Phautós tali a Balcsinál 2025 Augusztus 2 napján (szombat)
- KRTLPC: Ki és hogyan élt túl? Volt ám fennakadás
- Rap, Hip-hop 90'
- Gurulunk, WAZE?!
Hirdetés
Talpon vagyunk, köszönjük a sok biztatást! Ha segíteni szeretnél, boldogan ajánljuk Előfizetéseinket!
Új hozzászólás Aktív témák
-

ESP
őstag
Srácok!
Van valami "kalkulátor" ? Többtagú kifejezések szorzásához?
pl: -4(5X-4)(3X-6)=
Ezt beírom is kidobja az eredményt?
-

Ruszki
senior tag
Üdv!
Gondolom ezt a képletet kellene használnom:
y=f'(x_0)(x-x_0)+f(x_0)
Egyszerűen nem esik le.....

-

#56474624
törölt tag
Az érintőegyenes meredeksége adott x_0 helyen megegyezik a derivált fv x_0 helyen vett értékével. Ez látszik, ha az (x_0, f(x_0)) pontból elkezded behúzni a grafikon húrjait. Ahogy egyre közeledsz x_0 - hoz, egyre jobban közelíted az érintőt. Egy ilyen húr által meghatározott differenciahányados pedig határértékben épp a derivált.
Tehát ismerjük az érintőegyenes meredekségét (f ' (x_0) ) és hogy átmegy az (x_0, f(x_0)) ponton. Ebből meghatározható az érintőegyenes egyenlete: f(x_0) = m * x_0 + b, ahol m = f ' (x_0) , b ebből kiszámítható. -

Ruszki
senior tag
Írja fel az f(x)=x^3-4x^2 függvény x0=2 helyhez tartozó érintőjének egyenletét!!!
Valaki tudna hozzá magyarázatot is írni,hogy MIÉRT!!??
Előre is köszönöm!
ui.:két pont koordinátáira meg találtam,hogy kell pl.: P(2,12) de ez nem esik le!
-

#56474624
törölt tag
válasz
 szatocs
#2988
üzenetére
szatocs
#2988
üzenetére
Az A^n mátrix első sorának első elemére áll a következő:
2 * (A^(n-1) mátrix első sorának első eleme) + (-1)^n * 2
Aztán az első sor második elemére:
2 * (A^(n-1) mátrix első sorának első eleme) + (-1)^n
Második sor első elemére:
2 * (A^(n-1) mátrix második sorának első eleme) + (-1)^(n+1) * 2
Második sor második elemére:
2 * (A^(n-1) mátrix második sorának első eleme) + (-1)^(n+1)
Ez a felírás így jó (ha nem néztem el vmit), a gond csak az, hogy rekurzív, nekünk pedig explicit képlet kellene.
Általánosan felírva pl. az első sor első elemére:
X_n = 2*X_(n-1) + (-1)^n * 2Ez átírható a következő alakba a váltakozó előjelet kiküszöbölve:
X_n - X_(n-1) = 2 * X_(n-2)
(Ez az előzőből következik amennyiben mindkét oldalból kivonunk X_(n-1)-et.)
Ez a kettes szorzót leszámítva eléggé hasonlít a Fibonacci-ra, az explicit képlet ahhoz hasonló módon kihozható szerintem, de én most ehhez lusta vagyok, meg nem is nagyon emlékszem már.
-

szatocs
őstag
Sziasztok!
A következő mátrixnak kellene kiszámolnom az n-edik hatványát (jelen esetben 2012-ik):
(0 1; 2 1)
Eddig jutottam el, észrevettem egy azonosságot, az előző hatvány alsó sorával és a következő hatvány felső sorával kapcsolatban (megegyeznek), valamint az adott hatvány felső sorával és az adott hatvány alsó sorával kapcsolatban. Páros és páratlan hatványonként az adott hatvány mátrixának felső és alsó sora között van egy előjel váltásnyi változás.
Innen viszont nem tudom továbbvinni, hogy hogyan lehetne képletbe foglalni az n-edik hatvány képletét, attól függően, hogy páros vagy páratlan az adott hatvány.
Tud valaki erre valami azonosságot vagy bármit, ami mentél el lehetne indulni? Néztem a Jordán normálalakot is, de sehogy sem tudok rájönni, hogy hogyan lehetne kiszámolni a páros és a páratlan hatványokra vonatkozó egyenletet, valamint a 2012. hatványt.
-

bubi92
őstag
Sziasztok!
Megtudnátok mondani, hogy ez így okés-e Illetve a Konvexitást nem vágom...
Illetve a Konvexitást nem vágom...1. Értelmezési tartomány
Df = R {-3.33}
2. Zérus hely
A fv.-nek nincsenek zérus helyei, nem érinti az X tengelyt
3. Monotonitás
x<-6.65 szigorúan monoton növekedő
-6.65<x<-0.58 szigorúan monoton csökkenő
x<-0.58 szigorúan monoton növekedő
4. Szélsőérték
Helyi max: (-6.65, -4.31)
Helyi min: (-0.58, 9.79)
5. Konvexitás6. Inflexiós pont
Nincsen inflexiós pont, mert a fv. 2. deriváltja nem érinti az X tengelyt
7. Határérték -ben (vagy az ért.tart. végpontjaiban) és a szakadási helyeken
A szakadási helyeken: Jobbról:∞,Balról: -∞
+- ∞-ben: a határérték nem definiált
8. Abszolút szélsőérték
A fv.-nek nincsen abszolút szélsőértéke
9. Értékkészlet
Rf= -+∞ -

#56474624
törölt tag
válasz
 Jester01
#2985
üzenetére
Jester01
#2985
üzenetére
Közben sikerült megoldanom végre. Ha egyedül akarsz rájönni, ne olvass tovább, off-ba is teszem.

Ebből indultunk ki: x^2 + ( (5x) / (x-5) )^2 = 11.
[x + (5x)/(x-5)]^2 - [10x^2 + 11(x-5)] / (x-5) = 0
[(x(x-5) + 5x)^2 - 10(x^2)*(x-5) - 11(x-5)^2] / (x-5)^2 = 0
[x^2 - 5(x-5)]^2 - 36(x-5)^2 = 0
[x^2 - 5(x-5) + 6(x-5)] * [x^2 - 5(x-5) - 6(x-5)] = 0.
Az első tag megoldása adja a két valós, a másodiké a két komplex gyököt.
-
Üdv!
Gyors segítség kéne, mert rég volt már:
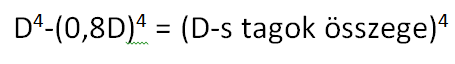
Hogy néz ki a D-s tagos összege ilyen esetben? Előre is köszi!
-

Ruszki
senior tag
Üdv!
Próbálok deriválást tanulni de elakadtam!

A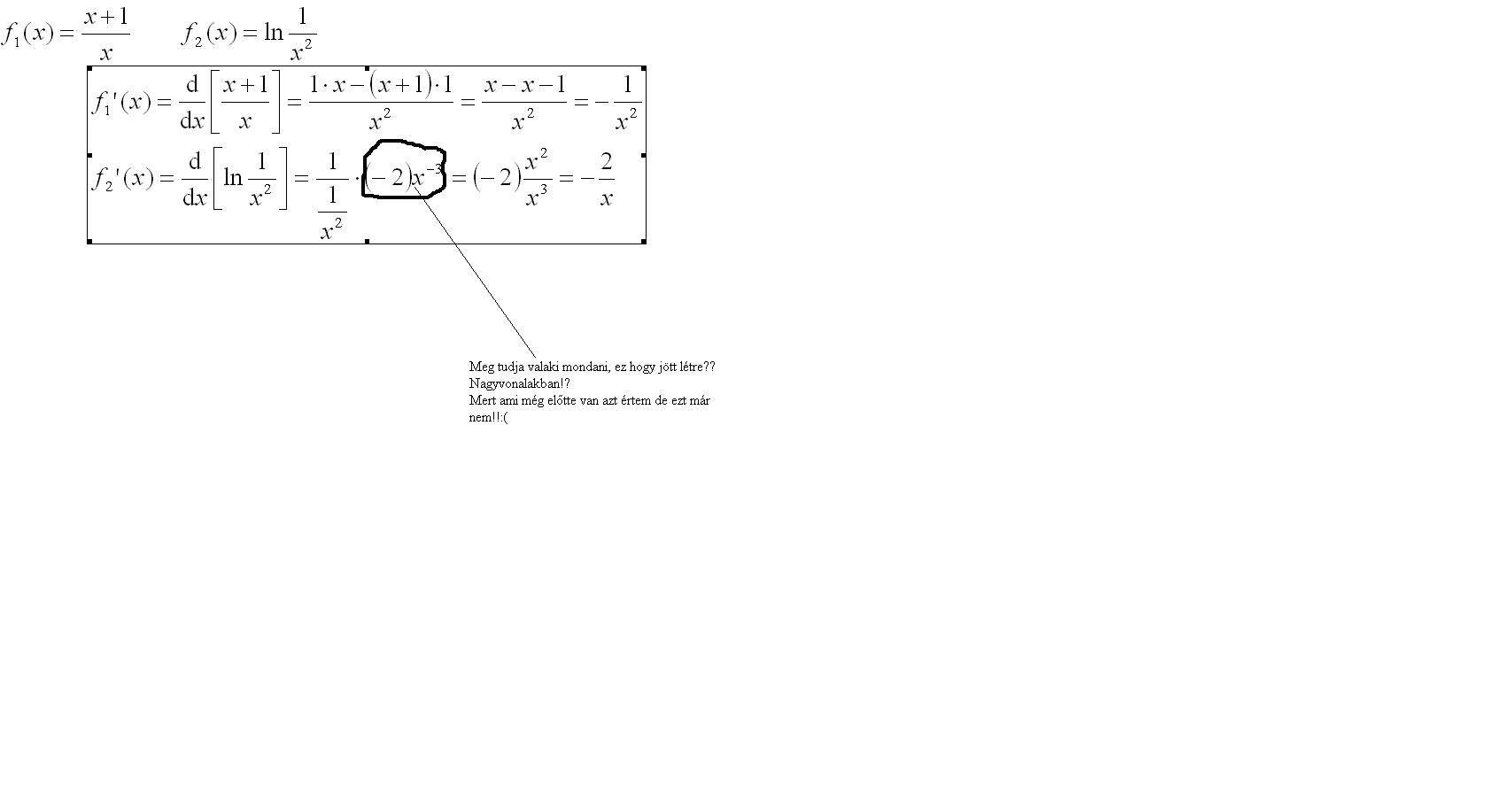 látható,hogy hol!
látható,hogy hol!
Ha valaki nagy vonalakban elmagyarázná akár pm-ben is, megköszönném! -

#56474624
törölt tag
válasz
 Jester01
#2979
üzenetére
Jester01
#2979
üzenetére
Nem hiszem, hogy ez kör.
Ez egy függvény (konkrétan (5x) / (x-5) ), aminek bizonyos pontjaira teljesül, hogy a távolságuk az origótól gyök11. A megoldások ismeretében (két valós, két komplex gyök) különben biztos, hogy negyedfokú is marad, csak valószínűleg valami "szép" negyedfokú (tehát elvileg felbomlik egy "x-tengelyt kétszer metsző" másodfokú, és egy "x-tengelyt nem metsző" másodfokú szorzatára).
Póbáltam úgy is, hogy polárkoordinátákra átírom az (5x) / (x-5) - öt, de a csöbörből-vödörbe esete állt elő.
-

#56474624
törölt tag
Eszembe jutott ez a területes trükk, de a megvalósításig már nem jutottam el lustasági okokból.
 Meg nagyon a koszinusztételre hajtottam, miután mondta, hogy ezt tanulták. Úgy viszont elég undorító dolgok jönnek ki.
Meg nagyon a koszinusztételre hajtottam, miután mondta, hogy ezt tanulták. Úgy viszont elég undorító dolgok jönnek ki. 
Akkor most én adnék fel egy feladatot, eddig még nem tudtam megcsinálni (negyedfokú persze könnyen kijön, de elvileg középiskolásan megoldható):
x^2 + ( (5x) / (x-5) )^2 = 11
(#2977) Jester01:
Másik ugyanez, csak "nagy" gyökjel előtt mínusz van.

-

Alg
veterán
válasz
 tvse1995
#2968
üzenetére
tvse1995
#2968
üzenetére
Na az egyik kolléga rájött
A két kis háromszög területe = nagy háromszög területe
azaz a*4*sin45/2 + b*4*sin45/2=a*b/2
sin45=gyök2/2-vel átrendezve
(a+b)*2*gyök2=a*b
legyen a+b=x, a*b=y
x^2 = a^2+b^2+2ab=100+2ab=100+2y=100+2*gyök2*x
Ez másodfokú x-re, megkapható y, ha pedig a+b és a*b ismert onnan mondjuk Viéte-formula...
-

Jester01
veterán
Haha én nyertem! A szerencsétlen kis harmadfokú egyenleted megfejelem egy negyedfokúval! Igaz abban már csak b van. Az online megoldóautomából kinyert eredmény úgy tűnik jó, mert szimmetrikus a-ra és b-re no és persze meg is szerkesztettem

De ahogy tanult szláv kollegám mondja, kell legyen egyszerűbb módja.
-

tvse1995
senior tag
Én közben a-t és b-t koszinusz tételből kifejezve majd behelyettesítve pit. tételbe egy nagyon hosszú polinomot kaptam amiben nincsenek egyforma tagok és még csak kiemelni sem lehet.
Közben írtam ez személyes bejegyzést is ahol szintén próbálkoznak: [link] Hátha megjön innen az ötlet.
-

Alg
veterán
egyik egyenlet, koszinusztétellel, cos45=gyök2/2:
[10a/(a+b)]^2=a^2 + 4^2 - 2*4*a*cos45
Ugyanez felírható a helyett b-re, amiből:
[10b/(a+b)]^2=b^2 + 4^2 - 2*4*b*cos45
Szerk: de elszámoltam
 szóval idáig jó ezzel kellene valamit kezdeni a^2 + b^2 = 100 is felhasználható ugyebár Pitagorasz
szóval idáig jó ezzel kellene valamit kezdeni a^2 + b^2 = 100 is felhasználható ugyebár Pitagorasz -

Alg
veterán
válasz
 tvse1995
#2964
üzenetére
tvse1995
#2964
üzenetére
két kis háromszög:
Egyiknél egyik szög 45 fok, ennek két száránál lévő oldal 4 és a, harmadik oldal 10a/(a+b)
Másiknál szintén 45 fokos szög melletti oldalak 4 és b, harmadik oldal 10b/(a+b)
mindkettőre koszinusztétel 45 fokra és a,4 illetve b,4-re felírva.
Ez elvileg két egyenlet, két ismeretlen -

tvse1995
senior tag
Sziasztok,
adott egy ABC derékszögű háromszög. A 90fokos szög szögfelezőjéről tudjuk, hogy 4cm, arról az oldalról amit ez két részre oszt arról pedig, hogy 10cm.
Ezekből az adatokból kéne kiszámolni a háromszög szögeit és oldalait.A témakörünk a szinusz és koszinusz tétel tehát ezekkel próbáltam kezdeni valamit de egyelőre nem sok sikerrel.

Előre köszi.

-

Sleed
aktív tag
válasz
 Jester01
#2955
üzenetére
Jester01
#2955
üzenetére
tehát megvan user1 és user2 adatom,megkapom átlag1-et és átlag2-t (legyen a második a fontosabb), és kiszámolom |átlag1-user1|+|átlag2-user2|*1,4 értéket minden userre, és akié a legkisebb, az van a legközelebb, ugye?
így már értem, köszönöm a segítséget.
bandus: igazából le kell programoznom

-

malwy
senior tag
Sziasztok!
Egyszerűen nem jövök rá, muszáj segítséget kérnem.[f(x)]^^3 + 3*f(x)=x
Mi a megoldás és miért egyértelmű? Bizonyítás kellene igazából, de már megoldás elég lenne

-

Sleed
aktív tag
Sziasztok, a segítségeteket szeretném kérni.
Adott 9 ember, mindenkihez két százalékos adat van rendelve.
Kiszámoljuk mindkét adatból az átlagot, és meg szeretnénk tudni, hogy ki van a legközelebb az átlaghoz úgy, hogy az egyik adatnak a súlya 1,4szerese a másikénak.Fogalmam sincs, hogy fogjak neki

Előre is köszönöm,
Sleed
-

akyyy
senior tag
wolframalpha-ba hogy kell beirni a függvényt, ha azt akarom hogy legyen ott egy hiperbola megy egy egyenes?
pl
x^2-y^2=1 és y=4 -

#56474624
törölt tag
válasz
 PumpkinSeed
#2949
üzenetére
PumpkinSeed
#2949
üzenetére
Nem 4 ismeretlenes inkább?
Gondolom azt kellene csinálni, hogy a vezéregyesek alatt ki szeretnéd nullázni.
Ehhez első sort leosztod annyival, hogy az első sor első eleme 1 legyen. Aztán a többi sorból kivonod az első sor annyiszorosát, hogy az adott sor első eleme 0 legyen. Ha ez megvan (ekkor már ugye az első oszlop egy 1-essel kezdődik, alatta 0-k), akkor a második sornál is eljátszod ugyanezt: leosztod annyival, hogy a második sor második eleme 1 legyen. Majd szépen kinullázod alatta végig. Stb. -

PumpkinSeed
addikt
Tudna nekem valaki segíteni?
Adott egy 3x4-es mátrix, amelyben egy 3 ismeretlenes egyenletrendszer van leírva. Felső 3szöges mátrixxal akarom megoldani, de viszont nem nagyon értem, hogy hogy van ez a 0-ra rendezés.
-

#56474624
törölt tag
Az ABC háromszög területe egység. Az E, F és G pontok rendre a BC, CA, ill. AB oldalakon vannak úgy, hogy AE az R pontban felezi BF-et, BF az S pontban felezi CG-t, CG a T-ben felezi AE-t. Mekkora az RST háromszög területe?
(én már megcsináltam, csak mint szép feladat raktam be az unatkozóknak
 )
) -

PumpkinSeed
addikt
válasz
 PindurAnna
#2946
üzenetére
PindurAnna
#2946
üzenetére
Ha így halad akkor nem lesz szükség arra, hogy valakire is támaszkodjon taníttatás szempontjából, mert ösztöndíjjal bárhova felveszik és amellett ha vállal gépészetben munkát akkor jó sorsa lesz. Sok sikert neki.
Elnézést az OFF-ért.

-

PindurAnna
Közösségépítő
válasz
 PumpkinSeed
#2945
üzenetére
PumpkinSeed
#2945
üzenetére
Itt helyben a legerősebb középiskolába..két nyelvű gépész szakra a Mechwart András Szakközépiskolába. Informatika szak is van ebbe a suliba, de mire azt kitanulja annyi lesz , mint égen a csillag. A gépész szak 6 éves és akkor német tanárok előtt nemzetközi szintű technikusi vizsgát tehet. Ha nem tudom tovább taníttatni, akkor szerintem ezzel is jól fog keresni, akár itthon, akár külföldön.
-

PumpkinSeed
addikt
válasz
 PindurAnna
#2944
üzenetére
PindurAnna
#2944
üzenetére
Gratula neki. Az szép teljesítmény. Nem akarok tolakvó lenni, de milyen szakra megy tanulni?

-

PindurAnna
Közösségépítő
válasz
 PumpkinSeed
#2943
üzenetére
PumpkinSeed
#2943
üzenetére
Gimnáziumi levelező versenysorozat egyik feladata..de hirtelen és sem tudtam hogy fogjunk hozzá

Szerencsére kitűnő tanuló, és pár napja kapta meg Debrecen város tehetséges diákjai címet

Nagyon büszke is vagyok rá

-

PumpkinSeed
addikt
válasz
 PindurAnna
#2940
üzenetére
PindurAnna
#2940
üzenetére
Csak érdekelt, mert én bár 2 éve nem tanultam matematikát okj-s hálózatépítőként nem tudtam ezt a feladatot.
 Nagyon ügyes lehet ha már ilyen feladatokat kap.
Nagyon ügyes lehet ha már ilyen feladatokat kap.  Ellenben velem
Ellenben velem
-

PindurAnna
Közösségépítő
válasz
 PumpkinSeed
#2939
üzenetére
PumpkinSeed
#2939
üzenetére
8, miért?
-

PumpkinSeed
addikt
válasz
 PindurAnna
#2938
üzenetére
PindurAnna
#2938
üzenetére
Megkérdezhetném, hogy hanyadikos a fiad?

-

Jester01
veterán
válasz
 PindurAnna
#2936
üzenetére
PindurAnna
#2936
üzenetére
Hát miért nem vettél neki építőkockákat

Na, építsünk tornyokat. Minden magasságnál tartsuk nyilván hány olyan van aminek piros a teteje és hány aminek fehér. Amikor a következő emeletet ráhúzzuk, akkor pirosat bármilyenre tehetünk de fehéret csak pirosra. Tehát ha P, F az előző és P', F' az új emelet, akkor P'=P+F és F'=P.
Mindenki kicsiben kezdi, nézzük az 1 emeletes tornyokat. Nyilván 1 piros tetejű és 1 fehér tetejű a választék, ezt (1,1) formában írom. Innentől már csak a fentebb megállapított szabályt kell alkalmazni (Rózsa György-féle "Kapcsoltam" stílusban: ez első számból lesz a második, az új első pedig a két régi összege):
1: (1,1)
2: (2,1)
3: (3,2)
4: (5,3)
5: (8,5)
6: (13,8)
7: (21,13)
8: (34,21)
9: (55,34)
10: (89,55)Tehát 10 emeletesből van 89 aminek piros a teteje és 55 aminek fehér, ez összesen 144.
-

PindurAnna
Közösségépítő
Sziasztok. Ebben a feladatban kellene nekem segítség, mert nem tudok a fiamnak segíteni benne:
Petinek piros és fehér (egyforma méretű) Lego kockái vannak. Ezekből tízemeletes tornyokat szeretne építeni, de úgy, hogy két fehér színű szint (kocka) ne kerüljön egymásra. Pirosból akármennyi is lehet egymás fölött. Hány különböző tornyot építhet Peti?
Köszönöm.
-

artiny
őstag
Van egy számítas amiben ismént elakadtam:
√((3/L)g) * (L/2)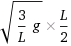
és az eredémy ha minden igaz erre jött ki:
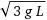
-

Jester01
veterán
A második egyenlet alapján (T1-T2)-t helyettesítették az elsőbe, mi a probléma?
(1/2)*m*R*a = R (g(m1 - m2) - a(m1 + m2)) - M = Rg(m1-m2) - Ra(m1 + m2) - M
(1/2)mRa + (m1+m2)Ra = Rg(m1-m2) - M
(1/2)ma + (m1+m2)a=g(m1-m2) - M/R
(m/2 + m1 + m2)a=g(m1-m2) - M/R
a = (g(m1-m2) - M / R) / (m/2 + m1 + m2) -

artiny
őstag
Fizika peldaban - van ket egynelet amibol a vegen kifejezik az "a" -t. Hogyan jutottak el az a -ig?
(1/2)*m*R*a = R (T1 - T2) - M
T1 - T2 = g(m1 - m2) - a(m1 + m2)
az "a" erre jött ki:
a = ( g(m1 - m2) - M/R ) / ( m1 + m2 + 1/2m )
-

Arpee78
senior tag
Valaki levezetné nekem ezt az egyenletet? A gamma kiszámolására lennék kíváncsi, tehát gamma legyen egy oldalon: gamma = ???
a és b egyszerű szám. Alfa, béta és gamma pedig szög.
a * gyök(tan²(alfa) + tan²(gamma) +1) = b * gyök(tan²(béta) + tan²(90-gamma) +1)
-

Jester01
veterán
válasz
 zuzu000
#2921
üzenetére
zuzu000
#2921
üzenetére
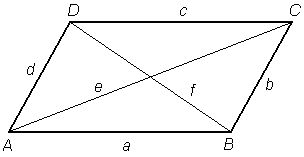
Ugye a paralelogramma átlói felezik egymást, mivel a szembenlévő AOB és COD háromszögek egybevágóak (O a metszéspont). Ha ezen felül még merőlegesek is, akkor mind a 4 O csúcsú háromszög egybevágó (két oldal és a közrezárt szög azonos). Ha pedig egybevágóak akkor értelemszerűen a paralelogramma minden oldala egyforma hosszú és ezért rombusz.
-

Jester01
veterán
válasz
 Bjørgersson
#2919
üzenetére
Bjørgersson
#2919
üzenetére
Nem
 , egy matematikus biztos talált volna egyszerűbb megoldást.
, egy matematikus biztos talált volna egyszerűbb megoldást.Egyébként tessék vigyázni, mert az egyik sort érdekesen nem törte el a fórummotor, úgyhogy íme mégegyszer:
r = TAPQ / (AP + PQ / 2) =
= (5/18 * a^2) / (gyök(13)/3 * a + gyök(2) / 6 * a) =
= 5/18 / (gyök(13)/3 + gyök(2) / 6) * a =
= 5 / (6gyök(13) + 3gyök(2)) * a ~ 0.19a. -

Jester01
veterán
válasz
 zuzu000
#2917
üzenetére
zuzu000
#2917
üzenetére
Szép feladat

A négyzet oldala legyen a.
Nézzük először az ABP háromszöget. A feladat szerint ennek a területe harmada a négyzetének, vagyis a*BP / 2 = a*a / 3, innen BP=2a/3. Ugyanígy DQ is, az AQD háromszögből, továbbá PC=CQ=a/3. PBE hasonló PCQ-hoz, tehát BE=BP=2a/3. ABS hasonló AEP-hez, vagyis AS / SP = AB / BE = a / (2a/3) = 3 / 2. Tehát az átló a szakaszokat 3 : 2 arányban osztja.A második részben az ASR háromszögbe beírt kör területe kellene. Ehhez előbb nézzük az APQ hasonló háromszöget, majd később arányosítjuk. Ismert képlet alapján a háromszög területe TAPQ=r * s = r * (AP + AQ + PQ) / 2 = r * (AP + PQ / 2), ahol r a beírt kör sugara, s pedig a fél kerület. Pitagorasz képlettel AP = gyök(a^2 + BP^2) = gyök(a^2 + 4a^2/9) = gyök(13)/3*a. PQ pedig gyök(2)/3*a. Továbbá TAPQ=TAPCQ - TPCQ=a^2/3 - a^2/18 = 5/18 * a^2. A beírt kör sugara tehát r = TAPQ / (AP + PQ / 2) = (5/18 * a^2) / (gyök(13)/3 * a + gyök(2) / 6 * a) = 5/18 / (gyök(13)/3 + gyök(2) / 6) * a = 5 / (6gyök(13) + 3gyök(2)) * a ~ 0.19a. Az ASR háromszög ugye 3/5 arányban kisebb, így a beírt kör sugara is, ami így kb. 0.11a. A kör területe a sugár négyzetével arányos, a négyzetbe pedig a/2 sugarú kör fér. Innen a kért arány már adódik, nagyjából (a^2/4) / (0.11a)^2 ~ 20 : 1, a pontos számítást az olvasóra bízom
![;]](//cdn.rios.hu/dl/s/v1.gif)
-

zuzu000
őstag
Hali!
Ezt valaki el tudna magyarazni, megoldani?
Egy negyzetet az egyik csucsabol indulo ket egyenes harom egyenlo teruletu reszre oszt.
a; Milyen aranyu reszekre osztja a ket egyenes negyzetbe eso szakaszat a szakaszokat metszo atlo?
b; Legyen a negyzetbe irt kor terulete T, a ket egyenes es az oket metszo atlp altal bezart haromszog beirt korenek terulete t. Hatarozzuk meg T:t erteket.Elore is koszi.
-

Jester01
veterán
válasz
 Apollo17hu
#2912
üzenetére
Apollo17hu
#2912
üzenetére
Mondjuk nem tudom miért javasolt, szerintem sokkal egyszerűbb kiszorozni/egyszerűsíteni.
Ha a hatványozást/gyökvonást írnák, akkor még érteném. -

Apollo17hu
őstag
Tankönyv luxus?
Még soha nem találkoztam ilyen exponenciális alakra alakítással, de Google első találata egy teljes könyvet dobott ki, amiben középiskolás szinten van leírva, hogy működik a dolog:
a konstans [5 vagy sqrt(5) a példádban] a valós és képzetes részből Pitagorasz-tétellel számolt "hossz" [sqrt(3^2+4^2) és sqrt(1^2+2^2)],
a hatványkitevő pedig az x-tengellyel bezárt szög (ami szögfüggvényekkel simán kiszámítható). -

artiny
őstag
válasz
 Apollo17hu
#2909
üzenetére
Apollo17hu
#2909
üzenetére

![;]](//cdn.rios.hu/dl/s/v1.gif) Köszi szépen a segitseged
Köszi szépen a segitseged 
-

Apollo17hu
őstag
-

Geryson
addikt
válasz
 Jester01
#2906
üzenetére
Jester01
#2906
üzenetére
Köszönöm nektek, akkor jó lesz a 45 fokos szög és akkor a felső oldala kicsit rövidebb lesz, mint terveztem. Viszont így megcsinálja a lapszabászat és nem kell asztalost vagy más egyebet keresnem...

(A korábbi hozzászólásomat telefonról írtam, ezért nem voltak ékezetek.)
-

artiny
őstag
MATEK - egyenletrendszer megoldásának utolsó lépésében mit csináltak, hogyan jött ki?
http://i.imgur.com/hIVVg.jpgnem ertem még azt sem hogy a végén hogyan emelnek ki,amikor kijott az utolso tort jel alatt a +R4 a nevezoben.
-

Geryson
addikt
Tudósok!

Kellene egy kis segítség. Adott egy egyenlő szárú trapéz, melynek a hosszabbik (alsó) oldala 188 cm, a rövidebbik (felső) oldala 120 cm. A két oldalsó oldal hossza 52 cm. A kérdésem az az, hogy hány fokos szöget zár be az oldalsó oldal a hosszú alsóhoz képest?
Azért kérdezek ilyen bonyolultat, mert egy bútorlapszabászatban szeretnék vágatni, de csak 45 fokos szöget tudnak vágni (a 90 fokos mellett) és nem tudom, hogy nekem ez jó-e. A következő kérdésem, hogy ha 45 fokos szöggel lőnénk be az oldalát, akkor mennyi lenne a felső hossz?
-
-

Jester01
veterán
válasz
 blackvinyl
#2900
üzenetére
blackvinyl
#2900
üzenetére
Az oldalban a hiba megtalálása meg biztos az informatika feladatsor része

Egyébként az eredmény tényleg –2,2 és el is fogadja, csak a mínusz jel az nem a szokásos hanem az unicode 2013 EN DASH. Másolj ki egy mínusz jelet a kérdésből, azzal jó lesz.
Új hozzászólás Aktív témák
- OHH! Dell Precision 7560 Tervező Vágó Laptop -70% 15,6" i7-11850H 32/1TB NVIDIA A3000 6GB FHD
- Ohh Lenovo ThinkPad P15 G2 Tervező Vágó Laptop -75% 15,6" i5-11500H 32/1TB RTX A2000 4GB /1 Millió/
- LÉZEREZÉS! külföldi billentyűzet magyarra kb. 20-30p alatt!
- Lian Li HydroShift 360 LCD /3x120mm RGB FAN/ HSLCD36RB (593933)
- Lian Li Hydroshift 360 LCD /FANLESS/ HSLCD36NB (593932)
- Dell latitude, precision, xps, magyar világítós billentyűzetek eladóak
- Intel Core i7-8700 / i7-9700 CPU, processzor - Számla, garancia
- LG 27MR400 - 27" IPS LED - 1920x1080 FHD - 100hz 5ms - AMD FreeSync - Villódzásmentes
- Telefon felvásárlás!! Samsung Galaxy S25, Samsung Galaxy S25 Plus, Samsung Galaxy S25 Ultra
- Telefon felvásárlás!! Samsung Galaxy S25, Samsung Galaxy S25 Plus, Samsung Galaxy S25 Ultra











 )
)




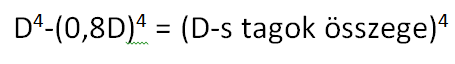








 szóval idáig jó ezzel kellene valamit kezdeni a^2 + b^2 = 100 is felhasználható ugyebár Pitagorasz
szóval idáig jó ezzel kellene valamit kezdeni a^2 + b^2 = 100 is felhasználható ugyebár Pitagorasz













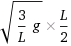
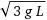




 , egy matematikus biztos talált volna egyszerűbb megoldást.
, egy matematikus biztos talált volna egyszerűbb megoldást.


![;]](http://cdn.rios.hu/dl/s/v1.gif)








 axioma
axioma